Refine listing
Actions for selected content:
2838 results in 11xxx
An improvement of Artin's conjecture on average for composite moduli
- Part of
-
- Journal:
- Mathematika / Volume 51 / Issue 1-2 / December 2004
- Published online by Cambridge University Press:
- 26 February 2010, pp. 97-109
- Print publication:
- December 2004
-
- Article
- Export citation
The unreasonable effectualness of continued function expansions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 3 / December 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 305-320
- Print publication:
- December 2004
-
- Article
-
- You have access
- Export citation
On a problem of Granville and Zhu Regarding Pascal's triangle
- Part of
-
- Journal:
- Mathematika / Volume 51 / Issue 1-2 / December 2004
- Published online by Cambridge University Press:
- 26 February 2010, pp. 63-82
- Print publication:
- December 2004
-
- Article
- Export citation
On f(n) modulo Ω(n) and ω(n) when f is a polynomial
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 2 / October 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 149-164
- Print publication:
- October 2004
-
- Article
-
- You have access
- Export citation
Integral points on elliptic curves over function fields
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 2 / October 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 197-208
- Print publication:
- October 2004
-
- Article
-
- You have access
- Export citation
A light-weight version of Waring's problem
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 3 / June 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 303-316
- Print publication:
- June 2004
-
- Article
-
- You have access
- Export citation
On decomposition of sub-linearised-polynomials
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 3 / June 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 317-328
- Print publication:
- June 2004
-
- Article
-
- You have access
- Export citation
The equation ω(n) = ω(n + 1)
- Part of
-
- Journal:
- Mathematika / Volume 50 / Issue 1-2 / December 2003
- Published online by Cambridge University Press:
- 26 February 2010, pp. 99-101
- Print publication:
- December 2003
-
- Article
- Export citation
Rational points on the superelliptic Erdös Selfridge curve of fifth degree
- Part of
-
- Journal:
- Mathematika / Volume 50 / Issue 1-2 / December 2003
- Published online by Cambridge University Press:
- 26 February 2010, pp. 113-124
- Print publication:
- December 2003
-
- Article
- Export citation
Counting points of bounded relative height
- Part of
-
- Journal:
- Mathematika / Volume 50 / Issue 1-2 / December 2003
- Published online by Cambridge University Press:
- 26 February 2010, pp. 125-152
- Print publication:
- December 2003
-
- Article
- Export citation
On a lattice point problem arising in the spectral analysis of periodic operators
- Part of
-
- Journal:
- Mathematika / Volume 50 / Issue 1-2 / December 2003
- Published online by Cambridge University Press:
- 26 February 2010, pp. 87-98
- Print publication:
- December 2003
-
- Article
- Export citation
Multiplicities of Higher Lie Characters
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 1 / August 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 9-21
- Print publication:
- August 2003
-
- Article
-
- You have access
- Export citation
Engel Series Expansions of Laurent Series and Hausdorff Dimensions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 1 / August 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-7
- Print publication:
- August 2003
-
- Article
-
- You have access
- Export citation
On The Asymptotic Values of Length Functions In Krull And Finitely Generated commutative Monoids
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 3 / June 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 421-436
- Print publication:
- June 2003
-
- Article
-
- You have access
- Export citation
Theta functions on Hermitian symmetric domains and fock representations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 2 / April 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 201-234
- Print publication:
- April 2003
-
- Article
-
- You have access
- Export citation
A simple remark on Dirichlet series
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 1 / February 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-4
- Print publication:
- February 2003
-
- Article
-
- You have access
- Export citation
Parametrizing simple closed geodesy on Γ3\ℋ
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 1 / February 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 43-60
- Print publication:
- February 2003
-
- Article
-
- You have access
- Export citation
Non-linear boundary value problems on the semi-infinite interval: an upper and lower solution approach
- Part of
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 129-140
- Print publication:
- June 2002
-
- Article
- Export citation
The universal quaternary quadratic form with the maximal discriminant
- Part of
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 197-199
- Print publication:
- June 2002
-
- Article
- Export citation
Density approximation and exact simulation of random variables that are solutions of fixed-point equations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 34 / Issue 2 / June 2002
- Published online by Cambridge University Press:
- 01 July 2016, pp. 441-468
- Print publication:
- June 2002
-
- Article
- Export citation
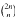 ends with
ends with 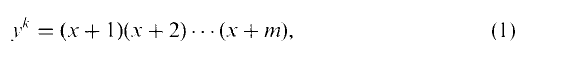
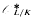 be the subgroup of the unit group
be the subgroup of the unit group 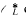 consisting of the elements that are roots of units of
consisting of the elements that are roots of units of 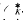 . Denote by
. Denote by 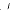 (
(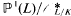 with relative height in the sense of Bergé-Martinet at most
with relative height in the sense of Bergé-Martinet at most 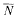 (ρ) the number
(ρ) the number 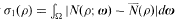 for dimensions
for dimensions 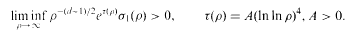
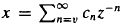 in an inderminate
in an inderminate 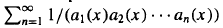 be the Engel expansin of Laurent series of
be the Engel expansin of Laurent series of 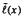 and
and 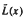 on
on 