Refine listing
Actions for selected content:
2838 results in 11xxx
Adiabatic limit of the eta invariant over cofinite quotients of PSL(2, ℝ)
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 6 / November 2008
- Published online by Cambridge University Press:
- 26 September 2008, pp. 1593-1616
- Print publication:
- November 2008
-
- Article
-
- You have access
- Export citation
On the lifting of hermitian modular forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 5 / September 2008
- Published online by Cambridge University Press:
- 01 September 2008, pp. 1107-1154
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
Stark–Heegner points and the Shimura correspondence
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 5 / September 2008
- Published online by Cambridge University Press:
- 01 September 2008, pp. 1155-1175
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
ON THE NUMBER OF REPRESENTATIONS OF INTEGERS BY CERTAIN QUADRATIC FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 129-140
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
A JOINT UNIVERSALITY THEOREM FOR PERIODIC HURWITZ ZETA-FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 13-33
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
ON THE BITS COUNTING FUNCTION OF REAL NUMBERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 85 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 95-111
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
ON THE NUMBER OF SIGN CHANGES OF HECKE EIGENVALUES OF NEWFORMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 85 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 87-94
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
JACOBI-LIKE FORMS, PSEUDODIFFERENTIAL OPERATORS, AND GROUP COHOMOLOGY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 55-71
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
On the unramified spectrum of spherical varieties over p-adic fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 4 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 978-1016
- Print publication:
- July 2008
-
- Article
-
- You have access
- Export citation
p-adic confluence of q-difference equations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 4 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 867-919
- Print publication:
- July 2008
-
- Article
-
- You have access
- Export citation
Frobenius fields for Drinfeld modules of rank 2
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 4 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 827-848
- Print publication:
- July 2008
-
- Article
-
- You have access
- Export citation
Global divisibility of Heegner points and Tamagawa numbers
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 4 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 811-826
- Print publication:
- July 2008
-
- Article
-
- You have access
- Export citation
MODULAR DIOPHANTINE INEQUALITIES AND ROTATIONS OF NUMERICAL SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 315-328
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
ON η3(aτ)η3(bτ) WITH a+b=8
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 301-313
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
Cohomology of topological groups with applications to the Weil group
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 3 / May 2008
- Published online by Cambridge University Press:
- 01 May 2008, pp. 633-656
- Print publication:
- May 2008
-
- Article
-
- You have access
- Export citation
Nearly ordinary Galois deformations over arbitrary number fields
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 1 / January 2009
- Published online by Cambridge University Press:
- 04 April 2008, pp. 99-177
- Print publication:
- January 2009
-
- Article
- Export citation
APPROXIMATION BY SEVERAL RATIONALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 325-329
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
Geometric Waldspurger periods
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 2 / March 2008
- Published online by Cambridge University Press:
- 01 March 2008, pp. 377-438
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
A dynamical version of the Mordell–Lang conjecture for the additive group
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 2 / March 2008
- Published online by Cambridge University Press:
- 01 March 2008, pp. 304-316
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
The arithmetic of Prym varieties in genus 3
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 2 / March 2008
- Published online by Cambridge University Press:
- 01 March 2008, pp. 317-338
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
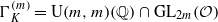 be the hermitian modular group of degree
be the hermitian modular group of degree 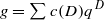 and
and 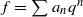 be modular forms of half-integral weight
be modular forms of half-integral weight 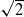 ,
, 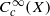 are in natural ‘almost bijection’ with a number of copies of
are in natural ‘almost bijection’ with a number of copies of 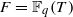 , with
, with 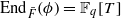 . Let
. Let 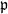 of good reduction for ϕ, let
of good reduction for ϕ, let 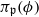 be a root of the characteristic polynomial of the Frobenius endomorphism of ϕ over the finite field
be a root of the characteristic polynomial of the Frobenius endomorphism of ϕ over the finite field 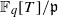 . Let Π
. Let Π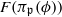 is the fixed imaginary quadratic field
is the fixed imaginary quadratic field 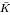 /
/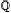 /ℚ) when
/ℚ) when 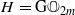 ,
, 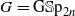 over
over 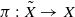 . Let
. Let 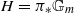 with
with 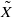 connected. We establish the geometric Langlands functoriality for this pair. Namely, we show that
connected. We establish the geometric Langlands functoriality for this pair. Namely, we show that 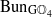 to
to 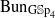 . Based on these calculations, we give three conjectural constructions of certain automorphic sheaves on
. Based on these calculations, we give three conjectural constructions of certain automorphic sheaves on 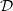 -modules only).
-modules only).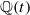 . By specialization, this also gives examples over
. By specialization, this also gives examples over 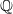 .
.