Refine listing
Actions for selected content:
2838 results in 11xxx
On the Eisenstein ideal for imaginary quadratic fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 3 / May 2009
- Published online by Cambridge University Press:
- 01 May 2009, pp. 603-632
- Print publication:
- May 2009
-
- Article
-
- You have access
- Export citation
q-series and weight 3/2 Maass forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 3 / May 2009
- Published online by Cambridge University Press:
- 01 May 2009, pp. 541-552
- Print publication:
- May 2009
-
- Article
-
- You have access
- Export citation
Formule du conducteur pour un caractère l-adique
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 3 / May 2009
- Published online by Cambridge University Press:
- 01 May 2009, pp. 687-717
- Print publication:
- May 2009
-
- Article
-
- You have access
- Export citation
Independence of points on elliptic curves arising from special points on modular and Shimura curves, II: local results
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 3 / May 2009
- Published online by Cambridge University Press:
- 01 May 2009, pp. 566-602
- Print publication:
- May 2009
-
- Article
-
- You have access
- Export citation
Mock Jacobi forms in basic hypergeometric series
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 3 / May 2009
- Published online by Cambridge University Press:
- 01 May 2009, pp. 553-565
- Print publication:
- May 2009
-
- Article
-
- You have access
- Export citation
ON THE LARGEST PRIME FACTOR OF THE MERSENNE NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 3 / June 2009
- Published online by Cambridge University Press:
- 17 April 2009, pp. 455-463
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
CODES ASSOCIATED WITH Sp(4,q) AND EVEN-POWER MOMENTS OF KLOOSTERMAN SUMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 3 / June 2009
- Published online by Cambridge University Press:
- 17 April 2009, pp. 427-435
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
ELEMENTARY PROOFS OF VARIOUS FACTS ABOUT 3-CORES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 3 / June 2009
- Published online by Cambridge University Press:
- 17 April 2009, pp. 507-512
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
QUALIFIED DIFFERENCE SETS FROM UNIONS OF CYCLOTOMIC CLASSES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 1 / August 2009
- Published online by Cambridge University Press:
- 17 April 2009, pp. 147-158
- Print publication:
- August 2009
-
- Article
-
- You have access
- Export citation
ON THE INDEX OF COMPOSITION OF THE EULER FUNCTION AND OF THE SUM OF DIVISORS FUNCTION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 01 April 2009, pp. 155-167
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
Local models in the ramified case. III Unitary groups
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 3 / July 2009
- Published online by Cambridge University Press:
- 26 March 2009, pp. 507-564
- Print publication:
- July 2009
-
- Article
- Export citation
EVALUATION OF CERTAIN CLASSES OF EISENSTEIN-TYPE SERIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 13 March 2009, pp. 239-247
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
ON THE GOWERS NORM OF PSEUDORANDOM BINARY SEQUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 13 March 2009, pp. 259-271
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
A Plancherel formula for Sp2n/Spn×Spn and its application
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 2 / March 2009
- Published online by Cambridge University Press:
- 01 March 2009, pp. 501-527
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
Primes with an average sum of digits
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 2 / March 2009
- Published online by Cambridge University Press:
- 01 March 2009, pp. 271-292
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
Brauer–Manin obstruction for integral points of homogeneous spaces and representation by integral quadratic forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 2 / March 2009
- Published online by Cambridge University Press:
- 01 March 2009, pp. 309-363
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
Intersection theory on Shimura surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 2 / March 2009
- Published online by Cambridge University Press:
- 01 March 2009, pp. 423-475
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
p-units in ray class fields of real quadratic number fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 2 / March 2009
- Published online by Cambridge University Press:
- 01 March 2009, pp. 364-392
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
ON SOME WEIGHTED AVERAGE VALUES OF L-FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 26 February 2009, pp. 183-186
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
Tate–Shafarevich groups in anticyclotomic ℤp-extensions at supersingular primes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 2 / March 2009
- Published online by Cambridge University Press:
- 19 February 2009, pp. 293-308
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
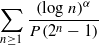
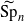 .
.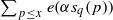 (where the sum is restricted to
(where the sum is restricted to 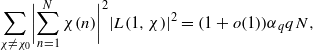
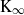 the anticyclotomic ℤ
the anticyclotomic ℤ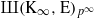 has trivial Λ-corank and, in the process, also show that
has trivial Λ-corank and, in the process, also show that 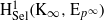 and
and  both have Λ-corank two.
both have Λ-corank two.