Refine listing
Actions for selected content:
2818 results in 11xxx
Statistics of the zeros of zeta functions in families of hyperelliptic curves over a finite field
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 11 December 2009, pp. 81-101
- Print publication:
- January 2010
-
- Article
-
- You have access
- Export citation
On some modular representations of the Borel subgroup of GL2(Qp)
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 11 December 2009, pp. 58-80
- Print publication:
- January 2010
-
- Article
-
- You have access
- Export citation
DISTRIBUTION OF INTEGER LATTICE POINTS IN A BALL CENTRED AT A DIOPHANTINE POINT
- Part of
-
- Journal:
- Mathematika / Volume 56 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 10 December 2009, pp. 118-134
- Print publication:
- January 2010
-
- Article
- Export citation
A NOTE ON THE SECOND MOMENT OF AUTOMORPHIC L-FUNCTIONS
- Part of
-
- Journal:
- Mathematika / Volume 56 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 10 December 2009, pp. 35-44
- Print publication:
- January 2010
-
- Article
- Export citation
NEW REPRESENTATIONS FOR APÉRY-LIKE SEQUENCES
- Part of
-
- Journal:
- Mathematika / Volume 56 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 10 December 2009, pp. 107-117
- Print publication:
- January 2010
-
- Article
- Export citation
SIMULTANEOUS DIOPHANTINE APPROXIMATION ON POLYNOMIAL CURVES
- Part of
-
- Journal:
- Mathematika / Volume 56 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 10 December 2009, pp. 77-85
- Print publication:
- January 2010
-
- Article
- Export citation
THE KAKEYA SET AND MAXIMAL CONJECTURES FOR ALGEBRAIC VARIETIES OVER FINITE FIELDS
- Part of
-
- Journal:
- Mathematika / Volume 56 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 10 December 2009, pp. 1-25
- Print publication:
- January 2010
-
- Article
- Export citation
On the probabilities of local behaviors in abelian field extensions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 08 December 2009, pp. 102-128
- Print publication:
- January 2010
-
- Article
-
- You have access
- Export citation
The Product of Exponents in the Factorization of Consecutive Integers
- Part of
-
- Journal:
- Mathematika / Volume 55 / Issue 1-2 / December 2009
- Published online by Cambridge University Press:
- 21 December 2009, pp. 59-65
- Print publication:
- December 2009
-
- Article
- Export citation
A Step Beyond Kemperman's Structure Theorem
- Part of
-
- Journal:
- Mathematika / Volume 55 / Issue 1-2 / December 2009
- Published online by Cambridge University Press:
- 21 December 2009, pp. 67-114
- Print publication:
- December 2009
-
- Article
- Export citation
The Artin–Carmichael Primitive Root Problem on Average
- Part of
-
- Journal:
- Mathematika / Volume 55 / Issue 1-2 / December 2009
- Published online by Cambridge University Press:
- 21 December 2009, pp. 167-176
- Print publication:
- December 2009
-
- Article
- Export citation
Exponential Squared Integrability of the Discrepancy Function in Two Dimensions
- Part of
-
- Journal:
- Mathematika / Volume 55 / Issue 1-2 / December 2009
- Published online by Cambridge University Press:
- 21 December 2009, pp. 1-27
- Print publication:
- December 2009
-
- Article
- Export citation
Regular and residual Eisenstein series and the automorphic cohomology of Sp(2,2)
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 23 November 2009, pp. 21-57
- Print publication:
- January 2010
-
- Article
-
- You have access
- Export citation
On volumes of arithmetic line bundles
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 6 / November 2009
- Published online by Cambridge University Press:
- 03 December 2009, pp. 1447-1464
- Print publication:
- November 2009
-
- Article
-
- You have access
- Export citation
On the parity of ranks of Selmer groups IV. With an appendix by Jean-Pierre Wintenberger
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 6 / November 2009
- Published online by Cambridge University Press:
- 03 December 2009, pp. 1351-1359
- Print publication:
- November 2009
-
- Article
-
- You have access
- Export citation
Sums of smooth squares
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 6 / November 2009
- Published online by Cambridge University Press:
- 03 December 2009, pp. 1401-1441
- Print publication:
- November 2009
-
- Article
-
- You have access
- Export citation
Produit eulérien motivique et courbes rationnelles sur les variétés toriques
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 6 / November 2009
- Published online by Cambridge University Press:
- 03 December 2009, pp. 1360-1400
- Print publication:
- November 2009
-
- Article
-
- You have access
- Export citation
ON m-COVERS AND m-SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 05 October 2009, pp. 223-235
- Print publication:
- April 2010
-
- Article
-
- You have access
- Export citation
SYLOW p-PSEUDOPRIMES TO SEVERAL BASES FOR SEVERAL PRIMES p
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 05 October 2009, pp. 165-176
- Print publication:
- February 2010
-
- Article
-
- You have access
- Export citation
FLAT PRIMES AND THIN PRIMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 26 April 2010, pp. 282-292
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
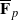 -representation
-representation 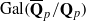 by using Fontaine’s theory of (φ,Γ)-modules. We compute Ω(
by using Fontaine’s theory of (φ,Γ)-modules. We compute Ω(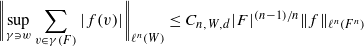
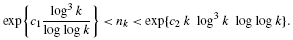
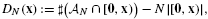
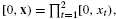 and |[
and |[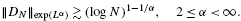
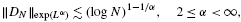
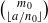 subsets
subsets 