Refine listing
Actions for selected content:
2838 results in 11xxx
On quadratic fields generated by the Shanks sequence
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 3 / October 2009
- Published online by Cambridge University Press:
- 23 September 2009, pp. 719-729
-
- Article
-
- You have access
- Export citation
The convergence of Euler products over p-adic number fields
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 3 / October 2009
- Published online by Cambridge University Press:
- 23 September 2009, pp. 583-606
-
- Article
-
- You have access
- Export citation
On Ihara’s lemma for Hilbert modular varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 5 / September 2009
- Published online by Cambridge University Press:
- 09 September 2009, pp. 1114-1146
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
Double Kernel Estimation of Sensitivities
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 3 / September 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 791-811
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
Stark units and the main conjectures for totally real fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 5 / September 2009
- Published online by Cambridge University Press:
- 23 October 2009, pp. 1163-1195
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
Hilbert modular forms and p-adic Hodge theory
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 5 / September 2009
- Published online by Cambridge University Press:
- 21 September 2009, pp. 1081-1113
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
Supersingular Kottwitz–Rapoport strata and Deligne–Lusztig varieties
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 11 August 2009, pp. 357-390
- Print publication:
- April 2010
-
- Article
- Export citation
The Gross–Kohnen–Zagier theorem over totally real fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 5 / September 2009
- Published online by Cambridge University Press:
- 10 August 2009, pp. 1147-1162
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
NONABELIAN NORMAL CM-FIELDS OF DEGREE 2pq
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 87 / Issue 1 / August 2009
- Published online by Cambridge University Press:
- 01 August 2009, pp. 129-144
- Print publication:
- August 2009
-
- Article
-
- You have access
- Export citation
Subconvexity bounds for automorphic L-functions
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 23 July 2009, pp. 95-124
- Print publication:
- January 2010
-
- Article
- Export citation
LIFTING PUZZLES IN DEGREE FOUR
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 1 / August 2009
- Published online by Cambridge University Press:
- 06 July 2009, pp. 65-82
- Print publication:
- August 2009
-
- Article
-
- You have access
- Export citation
QUASIMODULAR FORMS AND VECTOR BUNDLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 3 / December 2009
- Published online by Cambridge University Press:
- 02 July 2009, pp. 402-412
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
ELEMENTARY PROOFS OF PARITY RESULTS FOR 5-REGULAR PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 02 July 2009, pp. 58-63
- Print publication:
- February 2010
-
- Article
-
- You have access
- Export citation
ON THE CONJECTURE OF JEŚMANOWICZ CONCERNING PYTHAGOREAN TRIPLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 3 / December 2009
- Published online by Cambridge University Press:
- 02 July 2009, pp. 413-422
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
Perfect powers from products of consecutive terms in arithmetic progression
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 4 / July 2009
- Published online by Cambridge University Press:
- 01 July 2009, pp. 845-864
- Print publication:
- July 2009
-
- Article
-
- You have access
- Export citation
Level-raising for Saito–Kurokawa forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 4 / July 2009
- Published online by Cambridge University Press:
- 01 July 2009, pp. 915-953
- Print publication:
- July 2009
-
- Article
-
- You have access
- Export citation
Classification of two-dimensional split trianguline representations of p-adic fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 4 / July 2009
- Published online by Cambridge University Press:
- 01 July 2009, pp. 865-914
- Print publication:
- July 2009
-
- Article
-
- You have access
- Export citation
Poles of L-functions and theta liftings for orthogonal groups
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 4 / October 2009
- Published online by Cambridge University Press:
- 10 June 2009, pp. 693-741
- Print publication:
- October 2009
-
- Article
- Export citation
EIGHT CONSECUTIVE POSITIVE ODD NUMBERS NONE OF WHICH CAN BE EXPRESSED AS A SUM OF TWO PRIME POWERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 2 / October 2009
- Published online by Cambridge University Press:
- 08 June 2009, pp. 237-243
- Print publication:
- October 2009
-
- Article
-
- You have access
- Export citation
Overpartitions and the q-Bailey identity
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 28 May 2009, pp. 297-306
-
- Article
-
- You have access
- Export citation
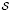 -unit equations as well as bounds for character sums to obtain a lower bound on the number of distinct fields among
-unit equations as well as bounds for character sums to obtain a lower bound on the number of distinct fields among 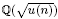 for
for 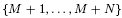 . Fields of this type include the Shanks fields and their generalizations.
. Fields of this type include the Shanks fields and their generalizations.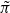 congruent to
congruent to 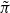 back to GSp(4), we use Arthur’s stable trace formula. Since
back to GSp(4), we use Arthur’s stable trace formula. Since 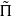 of GSp(4), congruent to Π, which is neither CAP nor endoscopic. It is crucial for our application that we can arrange for
of GSp(4), congruent to Π, which is neither CAP nor endoscopic. It is crucial for our application that we can arrange for 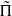 to have vectors fixed by the non-special maximal compact subgroups at all primes dividing
to have vectors fixed by the non-special maximal compact subgroups at all primes dividing 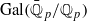 for
for 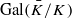 using
using 