Refine listing
Actions for selected content:
2838 results in 11xxx
Three-term arithmetic progressions and sumsets
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 02 February 2009, pp. 211-233
-
- Article
-
- You have access
- Export citation
A problem of Ozanam
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 02 February 2009, pp. 37-44
-
- Article
-
- You have access
- Export citation
On the Littlewood Problem Modulo a Prime
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 61 / Issue 1 / 01 February 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 141-164
- Print publication:
- 01 February 2009
-
- Article
-
- You have access
- Export citation
A NOTE ON THE FREIMAN AND BALOG–SZEMERÉDI–GOWERS THEOREMS IN FINITE FIELDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 01 February 2009, pp. 61-74
- Print publication:
- February 2009
-
- Article
-
- You have access
- Export citation
A deformation problem for Galois representations over imaginary quadratic fields
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 4 / October 2009
- Published online by Cambridge University Press:
- 30 January 2009, pp. 669-692
- Print publication:
- October 2009
-
- Article
- Export citation
Potential level-lowering for GSp(4)
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 3 / July 2009
- Published online by Cambridge University Press:
- 30 January 2009, pp. 595-622
- Print publication:
- July 2009
-
- Article
- Export citation
Presque Cp-représentations et (ϕ,Γ)-modules
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 4 / October 2009
- Published online by Cambridge University Press:
- 30 January 2009, pp. 653-668
- Print publication:
- October 2009
-
- Article
- Export citation
Ricci iterations on Kähler classes
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 4 / October 2009
- Published online by Cambridge University Press:
- 30 January 2009, pp. 743-768
- Print publication:
- October 2009
-
- Article
- Export citation
Wild ramification and the characteristic cycle of an ℓ-adic sheaf
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 4 / October 2009
- Published online by Cambridge University Press:
- 06 January 2009, pp. 769-829
- Print publication:
- October 2009
-
- Article
- Export citation
Geometric Weil representation: local field case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 1 / January 2009
- Published online by Cambridge University Press:
- 01 January 2009, pp. 56-88
- Print publication:
- January 2009
-
- Article
-
- You have access
- Export citation
Analytic vectors in continuous p-adic representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 1 / January 2009
- Published online by Cambridge University Press:
- 01 January 2009, pp. 247-270
- Print publication:
- January 2009
-
- Article
-
- You have access
- Export citation
The exceptional zero conjecture for Hilbert modular forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 1 / January 2009
- Published online by Cambridge University Press:
- 01 January 2009, pp. 1-55
- Print publication:
- January 2009
-
- Article
-
- You have access
- Export citation
ON THE DENSITY OF INTEGERS OF THE FORM (p−1)2−n IN ARITHMETIC PROGRESSIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 431-436
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
ARITHMETIC AND GEOMETRIC PROGRESSIONS IN PRODUCT SETS OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 357-364
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
Spectral numbers in Floer theories
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 6 / November 2008
- Published online by Cambridge University Press:
- 01 November 2008, pp. 1581-1592
- Print publication:
- November 2008
-
- Article
-
- You have access
- Export citation
Binary linear forms as sums of two squares
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 6 / November 2008
- Published online by Cambridge University Press:
- 01 November 2008, pp. 1375-1402
- Print publication:
- November 2008
-
- Article
-
- You have access
- Export citation
Chebyshev’s bias in function fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 6 / November 2008
- Published online by Cambridge University Press:
- 01 November 2008, pp. 1351-1374
- Print publication:
- November 2008
-
- Article
-
- You have access
- Export citation
Integral moments of automorphic L-functions
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 16 October 2008, pp. 335-382
- Print publication:
- April 2009
-
- Article
- Export citation
SUMS OF MULTIPLICATIVE FUNCTIONS OVER A BEATTY SEQUENCE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 327-334
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
A POLYNOMIAL APPROACH TO COCYCLES OVER ELEMENTARY ABELIAN GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 85 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 177-190
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
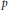
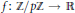
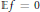
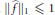
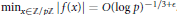
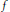
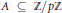
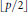
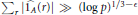
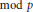
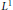

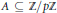
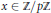
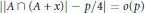
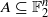 is such that ∣
is such that ∣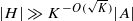 such that
such that 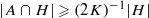 . Under the assumption that
. Under the assumption that 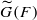 . This is a category of certain perverse sheaves on some stack, on which
. This is a category of certain perverse sheaves on some stack, on which 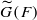 acts by functors. This construction will be used by Lysenko (in [
acts by functors. This construction will be used by Lysenko (in [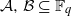 of elements of the finite field 𝔽
of elements of the finite field 𝔽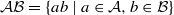
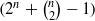 -dimensional GF(2
-dimensional GF(2