An asymptotic estimate is obtained for the number of partitions of the positive integer n into unequal parts coming from a sequence u, with each part greater than m, under suitable conditions on the sequence u. The estimate holds uniformly with respect to integers m such that 0 ≤ m ≤ n1−δ, as n → ∞, where δ is a given real number, such that 0 < δ < 1.

In this paper we compute and continue meromorphically to the whole complex plane the zeta function for twisted modular curves. The twist of the modular curve is done by a mod p representation of the absolute Galois group.

Suppose that {tn} is the sequence of positive roots of ζ (½ + it) counted according to multiplicity and arranged in non-decreasing order; in my paper [6] I proved that

and my main objective here is to improve this bound.

For each integer n ≥ 2, let β(n) be the sum of the distinct prime divisors of n and let (x) stand for the set of composite integers n ≤ x such that n is a multiple of β(n). Upper and lower bounds are obtained for the cardinality of (x).

This is a study of relations between pure cubic fields and their normal closures. Explicit formula shows how the discriminant, regulator and class number of the normal closure can be expressed in terms of the cubic field.

In this paper the absolute value or distance from the origin analogue of the classical Khintchine-Groshev theorem [5] is established for a single linear form with a “slowly decreasing” error function. To explain this in more detail, some notation is introduced. Throughout this paper, m, n are positive integers; i.e., m, n ∈ ℕ; x = (x1,…, xn) will denote a point or vector in ℝn, q = (q1,…, qn) will denote a non-zero vector in ℤn and

|x| := max{|x1|,…,|xn|} = ‖X‖∞

will denote the height of the vector x. Let Ψ : ℕ → (0, ∞) be a (non-zero) function which converges to 0 at ∞. The notion of a slowly decreasing functionΨ is defined in [3] as a function for which, given c ∈ (0, 1), there exists a K = K(c) > 1 such that Ψ(ck) ≤ KΨ(k). Of course, since Ψ is decreasing, Ψ(k) ≤ Ψ(ck). For any set X, |X| will denote the Lebesgue measure of X (there should be no confusion with the height of a vector).

In this paper is considered the average size of the 2-Selmer groups of a class of quadratic twists of each elliptic curve over ℚ with ℚ-torsion group ℤ2 × ℤ2. The existence is shown of a positive proportion of quadratic twists of such a curve, each of which has rank 0 Mordell-Weil group.

We study the distribution of principal ideals generated by irreducible elements in an algebraic number field.

In this paper, an improvement of a large sieve type inequality in high dimensions is presented, and its implications on a related problem are discussed.

In this paper, we give certain analytic functional relations for the double harmonic series related to the double Euler numbers. These can be regarded as continuous generalizations of the known discrete relations obtained by the author recently.

We remark on pseudo-elliptic integrals and on exceptional function fields, namely function fields defined over an infinite base field but nonetheless containing non-trivial units. Our emphasis is on some elementary criteria that must be satisfied by a squarefree polynomial D(x) whose square root generates a quadratic function field with non-trivial unit. We detail the genus I case.

A geometric mass concerning supersingular abelian varieties with real multiplications is formulated and related to an arithmetic mass. We determine the exact geometric mass formula for superspecial abelian varieties of Hubert-Blumenthal type. As an application, we compute the number of the irreducible components of the supersingular locus of some Hubert-Blumenthal varieties in terms of special values of the zeta function.

In this article we study some special problems of the additive number theory connected with an estimate of cardinality of a sum of two sets, which can be convex as well as non-convex sequences.

A two-bridge knot (or link) can be characterized by the so-called Schubert normal form Kp, q where p and q are positive coprime integers. Associated to Kp, q there are the Conway polynomial ▽kp, q(z) and the normalized Alexander polynomial Δkp, q(t). However, it has been open problem how ▽kp, q(z) and Δkp, q(t) are expressed in terms of p and q. In this note, we will give explicit formulae for the Conway polynomials and the normalized Alexander polynomials in the case of two-bridge knots and links. This is done using elementary number theoretical functions in p and q.

In this paper, we generalize the Kučera's group-determinant formulae to obtain the real and relative class number formulae of any subfield of cyclotomic function fields with arbitrary conductor in the form of a product of determinants. From these formulae, we generalize the relative class number formula of Rosen and Bae-Kang and obtain analogous results of Tsumura and Hirabayashi for an intermediate field in the tower of cyclotomic function fields with prime power conductor.

For the purpose of this paper, we call a set of positive reals ν a well-spaced set if there is a c > 0 such that

This article studies the non-homogeneous quadratic Bessel zeta function ζRB(s, v, a), defined as the sum of the squares of the positive zeros of the Bessel function Jv(z) plus a positive constant. In particular, explicit formulas for the main associated zeta invariants, namely, poles and residua ζRB(0, v, a) and ζRB(0, v, a), are given.

In this paper we study the pseudorandom properties of the signs of Kloosterman sums.

We provide a new probabilistic explanation for the appearance of Benford's law in everyday-life numbers, by showing that it arises naturally when we consider mixtures of uniform distributions. Then we connect our result to a result of Flehinger, for which we provide a shorter proof and the speed of convergence.

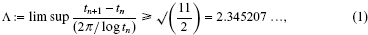
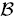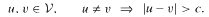
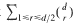The set ℳ* of numbers which occur as Mahler measures of integer polynomials and the subset ℳ of Mahler measures of algebraic numbers (that is, of irreducible integer polynomials) are investigated. It is proved that every number α of degree d in ℳ* is the Mahler measure of a separable integer polynomial of degree at most with all its roots lying in the Galois closure 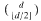F of ℚ(α), and every unit in ℳ is the Mahler measure of a unit in F of degree at most over ℚ This is used to show that some numbers considered earlier by Boyd are not Mahler measures. The set of numbers which occur as Mahler measures of both reciprocal and nonreciprocal algebraic numbers is also investigated. In particular, all cubic units in this set are described and it is shown that the smallest Pisot number is not the measure of a reciprocal number.