Refine listing
Actions for selected content:
2818 results in 11xxx
Unitary dual of GL(n) at archimedean places and global Jacquet–Langlands correspondence
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 5 / September 2010
- Published online by Cambridge University Press:
- 08 June 2010, pp. 1115-1164
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
ON A NONABELIAN BALOG–SZEMERÉDI-TYPE LEMMA
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 1 / August 2010
- Published online by Cambridge University Press:
- 08 June 2010, pp. 127-132
- Print publication:
- August 2010
-
- Article
-
- You have access
- Export citation
Approximate groups. I The torsion-free nilpotent case
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 10 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 02 June 2010, pp. 37-57
- Print publication:
- January 2011
-
- Article
- Export citation
Diagonal quartic surfaces and transcendental elements of the Brauer group
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 4 / October 2010
- Published online by Cambridge University Press:
- 28 May 2010, pp. 769-798
- Print publication:
- October 2010
-
- Article
- Export citation
Orbifoldes géométriques spéciales et classification biméromorphe des variétés kählériennes compactes
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 10 / Issue 4 / October 2011
- Published online by Cambridge University Press:
- 28 May 2010, pp. 809-934
- Print publication:
- October 2011
-
- Article
- Export citation
Le lemme fondamental pondéré. I. Constructions géométriques
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 6 / November 2010
- Published online by Cambridge University Press:
- 19 May 2010, pp. 1416-1506
- Print publication:
- November 2010
-
- Article
-
- You have access
- Export citation
ON THE MONTGOMERY–HOOLEY THEOREM IN SHORT INTERVALS
- Part of
-
- Journal:
- Mathematika / Volume 56 / Issue 2 / July 2010
- Published online by Cambridge University Press:
- 12 May 2010, pp. 231-243
- Print publication:
- July 2010
-
- Article
- Export citation
Swan conductors for p-adic differential modules. II Global variation
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 10 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 11 May 2010, pp. 191-224
- Print publication:
- January 2011
-
- Article
- Export citation
Explicit computations of Serre’s obstruction for genus-3 curves and application to optimal curves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 May 2010, pp. 192-207
-
- Article
-
- You have access
- Export citation
A lower bound for Garsia’s entropy for certain Bernoulli convolutions
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 May 2010, pp. 130-143
-
- Article
-
- You have access
- Export citation
Square-free values of quadratic polynomials
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 30 April 2010, pp. 385-392
-
- Article
-
- You have access
- Export citation
ON CARMICHAEL NUMBERS IN ARITHMETIC PROGRESSIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 3 / June 2010
- Published online by Cambridge University Press:
- 26 April 2010, pp. 313-321
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
On descent theory and main conjectures in non-commutative Iwasawa theory
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 10 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 26 April 2010, pp. 59-118
- Print publication:
- January 2011
-
- Article
- Export citation
Non-archimedean canonical measures on abelian varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 3 / May 2010
- Published online by Cambridge University Press:
- 21 April 2010, pp. 683-730
- Print publication:
- May 2010
-
- Article
-
- You have access
- Export citation
Schemes over 𝔽1 and zeta functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 6 / November 2010
- Published online by Cambridge University Press:
- 21 April 2010, pp. 1383-1415
- Print publication:
- November 2010
-
- Article
-
- You have access
- Export citation
On mean values and non-vanishing of derivatives of L-functions in a nonlinear family
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 20 April 2010, pp. 19-34
- Print publication:
- January 2011
-
- Article
-
- You have access
- Export citation
ON SHRINKING TARGETS FOR ℤm ACTIONS ON TORI
- Part of
-
- Journal:
- Mathematika / Volume 56 / Issue 2 / July 2010
- Published online by Cambridge University Press:
- 16 April 2010, pp. 193-202
- Print publication:
- July 2010
-
- Article
- Export citation
EULER NUMBERS MODULO 2n
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 09 April 2010, pp. 221-231
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
EXPANSION OF ORBITS OF SOME DYNAMICAL SYSTEMS OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 07 April 2010, pp. 232-239
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
Automorphisms of hyperelliptic modular curves X0(N) in positive characteristic
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 April 2010, pp. 144-163
-
- Article
-
- You have access
- Export citation
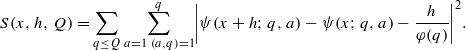
 , being a Jacobian over
, being a Jacobian over 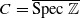 over 𝔽
over 𝔽 -schemes to interpret conceptually the spectral realization of zeros of
-schemes to interpret conceptually the spectral realization of zeros of 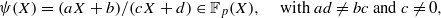
 of a modular curve
of a modular curve 