Refine listing
Actions for selected content:
2818 results in 11xxx
Modularity lifting theorems for Galois representations of unitary type
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 4 / July 2011
- Published online by Cambridge University Press:
- 18 March 2011, pp. 1022-1058
- Print publication:
- July 2011
-
- Article
-
- You have access
- Export citation
LINEAR FORMS AND QUADRATIC UNIFORMITY FOR FUNCTIONS ON 𝔽np
- Part of
-
- Journal:
- Mathematika / Volume 57 / Issue 2 / July 2011
- Published online by Cambridge University Press:
- 07 March 2011, pp. 215-237
- Print publication:
- July 2011
-
- Article
- Export citation
On expressible sets and p-adic numbers
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 25 February 2011, pp. 411-422
-
- Article
-
- You have access
- Export citation
The least common multiple of consecutive arithmetic progression terms
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 25 February 2011, pp. 431-441
-
- Article
-
- You have access
- Export citation
THE TRACE PROBLEM FOR TOTALLY POSITIVE ALGEBRAIC INTEGERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 3 / June 2011
- Published online by Cambridge University Press:
- 17 February 2011, pp. 341-354
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
Nonsolvable number fields ramified only at 3 and 5
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 3 / May 2011
- Published online by Cambridge University Press:
- 15 February 2011, pp. 716-734
- Print publication:
- May 2011
-
- Article
-
- You have access
- Export citation
Dichotomy for generic supercuspidal representations of G2
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 3 / May 2011
- Published online by Cambridge University Press:
- 15 February 2011, pp. 735-783
- Print publication:
- May 2011
-
- Article
-
- You have access
- Export citation
Sur le rang des courbes elliptiques sur les corps de classes de Hilbert
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 4 / July 2011
- Published online by Cambridge University Press:
- 10 February 2011, pp. 1087-1104
- Print publication:
- July 2011
-
- Article
-
- You have access
- Export citation
Serre weights for quaternion algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 4 / July 2011
- Published online by Cambridge University Press:
- 09 February 2011, pp. 1059-1086
- Print publication:
- July 2011
-
- Article
-
- You have access
- Export citation
A strengthening of the GL(2) converse theorem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 3 / May 2011
- Published online by Cambridge University Press:
- 07 February 2011, pp. 669-715
- Print publication:
- May 2011
-
- Article
-
- You have access
- Export citation
Iwasawa theory for modular forms at supersingular primes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 3 / May 2011
- Published online by Cambridge University Press:
- 07 February 2011, pp. 803-838
- Print publication:
- May 2011
-
- Article
-
- You have access
- Export citation
BOUNDS OF MULTIPLICATIVE CHARACTER SUMS WITH FERMAT QUOTIENTS OF PRIMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 3 / June 2011
- Published online by Cambridge University Press:
- 07 February 2011, pp. 456-462
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
A NOTE ON BADLY APPROXIMABLE LINEAR FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 04 February 2011, pp. 262-266
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
Degenerations and limit Frobenius structures in rigid cohomology
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 14 / 2011
- Published online by Cambridge University Press:
- 01 February 2011, pp. 1-33
-
- Article
-
- You have access
- Export citation
A NOTE ON FOURIER COEFFICIENTS OF POINCARÉ SERIES
- Part of
-
- Journal:
- Mathematika / Volume 57 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 21 December 2010, pp. 31-40
- Print publication:
- January 2011
-
- Article
- Export citation
ERDŐS–TURÁN WITH A MOVING TARGET, EQUIDISTRIBUTION OF ROOTS OF REDUCIBLE QUADRATICS, AND DIOPHANTINE QUADRUPLES
- Part of
-
- Journal:
- Mathematika / Volume 57 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 13 December 2010, pp. 1-29
- Print publication:
- January 2011
-
- Article
- Export citation
AN EXPLICIT INCIDENCE THEOREM IN 𝔽p
- Part of
-
- Journal:
- Mathematika / Volume 57 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 13 December 2010, pp. 135-145
- Print publication:
- January 2011
-
- Article
- Export citation
Extensions of rank one (φ,Γ)-modules and crystalline representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 2 / March 2011
- Published online by Cambridge University Press:
- 13 December 2010, pp. 375-427
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
The least common multiple of a quadratic sequence
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 4 / July 2011
- Published online by Cambridge University Press:
- 13 December 2010, pp. 1129-1150
- Print publication:
- July 2011
-
- Article
-
- You have access
- Export citation
EFFICIENTLY GENERATED SPACES OF CLASSICAL SIEGEL MODULAR FORMS AND THE BÖCHERER CONJECTURE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 3 / December 2010
- Published online by Cambridge University Press:
- 01 April 2011, pp. 393-405
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
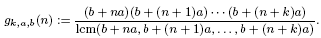
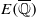 contains Heegner points of discriminant
contains Heegner points of discriminant 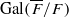 which is modular in the sense that it comes from an automorphic form on a definite quaternion algebra with centre
which is modular in the sense that it comes from an automorphic form on a definite quaternion algebra with centre 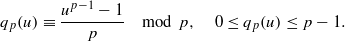
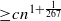 lines, where
lines, where 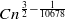 , where
, where 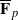 -representations of
-representations of 