Refine listing
Actions for selected content:
2818 results in 11xxx
SUM–PRODUCT ESTIMATES AND MULTIPLICATIVE ORDERS OF γ AND γ+γ−1 IN FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 30 November 2011, pp. 505-508
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
A twisted topological trace formula for Hecke operators and liftings from symplectic to general linear groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 09 November 2011, pp. 65-120
- Print publication:
- January 2012
-
- Article
-
- You have access
- Export citation
ON THE CONSECUTIVE POWERS OF A PRIMITIVE ROOT: GAPS AND EXPONENTIAL SUMS
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 08 November 2011, pp. 11-20
- Print publication:
- January 2012
-
- Article
- Export citation
On the AF-algebra of a Hecke eigenform
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 08 November 2011, pp. 207-213
-
- Article
-
- You have access
- Export citation
Proving the Birch and Swinnerton-Dyer conjecture for specific elliptic curves of analytic rank zero and one
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 14 / 2011
- Published online by Cambridge University Press:
- 01 November 2011, pp. 327-350
-
- Article
-
- You have access
- Export citation
Algebraic integers as special values of modular units
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 01 November 2011, pp. 167-179
-
- Article
-
- You have access
- Export citation
ON THE DISTRIBUTION OF GALOIS GROUPS
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 21 October 2011, pp. 35-44
- Print publication:
- January 2012
-
- Article
- Export citation
AN EXTENSION OF SURY’S IDENTITY AND RELATED CONGRUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 04 October 2011, pp. 482-496
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
Cohomologie d’intersection des variétés modulaires de Siegel, suite
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 6 / November 2011
- Published online by Cambridge University Press:
- 28 September 2011, pp. 1671-1740
- Print publication:
- November 2011
-
- Article
-
- You have access
- Export citation
SUMSETS AND DIFFERENCE SETS CONTAINING A COMMON TERM OF A SEQUENCE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 26 September 2011, pp. 79-83
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
POWER-FREE VALUES OF THE POLYNOMIAL t1⋯tr−1
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 23 September 2011, pp. 154-163
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
SUMS OF DISTINCT INTEGRAL SQUARES IN
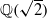 ,
, 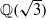 AND
AND 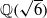
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 08 September 2011, pp. 1-10
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
RATIONAL POINTS ON THREE SUPERELLIPTIC CURVES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 06 September 2011, pp. 105-113
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
Some unlikely intersections beyond André–Oort
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 30 August 2011, pp. 1-27
- Print publication:
- January 2012
-
- Article
-
- You have access
- Export citation
Remarks on endomorphisms and rational points
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 6 / November 2011
- Published online by Cambridge University Press:
- 24 August 2011, pp. 1819-1842
- Print publication:
- November 2011
-
- Article
-
- You have access
- Export citation
On simultaneous rational approximation to a p-adic number and its integral powers
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 3 / October 2011
- Published online by Cambridge University Press:
- 17 August 2011, pp. 599-612
-
- Article
-
- You have access
- Export citation
Families of explicitly isogenous Jacobians of variable-separated curves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 14 / 2011
- Published online by Cambridge University Press:
- 01 August 2011, pp. 179-199
-
- Article
-
- You have access
- Export citation
Computations with classical and p-adic modular forms
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 14 / 2011
- Published online by Cambridge University Press:
- 01 August 2011, pp. 214-231
-
- Article
-
- You have access
- Export citation
ON HYBRID SEQUENCES BUILT FROM NIEDERREITER–HALTON SEQUENCES AND KRONECKER SEQUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 2 / October 2011
- Published online by Cambridge University Press:
- 29 July 2011, pp. 238-254
- Print publication:
- October 2011
-
- Article
-
- You have access
- Export citation
The sign of Galois representations attached to automorphic forms for unitary groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 27 July 2011, pp. 1337-1352
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
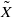 by gluing together 2
by gluing together 2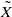 and get formulas for the traces of Hecke operators ℋ acting on the cohomology of
and get formulas for the traces of Hecke operators ℋ acting on the cohomology of 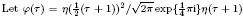 , where
, where 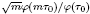 is an algebraic integer dividing
is an algebraic integer dividing 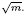 This is a generalization of a result of Berndt, Chan and Zhang. On the other hand, when
This is a generalization of a result of Berndt, Chan and Zhang. On the other hand, when 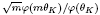 is a unit.
is a unit.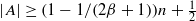 , then (
, then (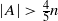 , then (
, then ( cannot be improved.
cannot be improved.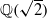 ,
, 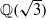 AND
AND 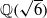
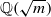 which can be represented as sums of distinct integral squares, where
which can be represented as sums of distinct integral squares, where 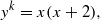
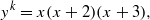
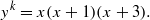
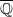 . Finally, we formulate and prove a variant of the Mordell–Lang conjecture for subvarieties of
. Finally, we formulate and prove a variant of the Mordell–Lang conjecture for subvarieties of 