Refine listing
Actions for selected content:
2818 results in 11xxx
IRRATIONALITY AND NONQUADRATICITY MEASURES FOR LOGARITHMS OF ALGEBRAIC NUMBERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 22 November 2012, pp. 237-267
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
ON THE EQUATION f(g(x))=f(x)hm(x) FOR COMPOSITE POLYNOMIALS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 19 September 2012, pp. 155-161
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
ON TORSION OF CLASS GROUPS OF CM TORI
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 2 / July 2012
- Published online by Cambridge University Press:
- 28 March 2012, pp. 305-318
- Print publication:
- July 2012
-
- Article
- Export citation
A PAUCITY ESTIMATE RELATED TO NEWTON SUMS OF ODD DEGREE
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 2 / July 2012
- Published online by Cambridge University Press:
- 27 March 2012, pp. 225-235
- Print publication:
- July 2012
-
- Article
- Export citation
HUA-TYPE ITERATION FOR MULTIDIMENSIONAL WEYL SUMS
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 2 / July 2012
- Published online by Cambridge University Press:
- 27 March 2012, pp. 209-224
- Print publication:
- July 2012
-
- Article
- Export citation
ON PAIRS OF LINEAR EQUATIONS IN FOUR PRIME VARIABLES AND POWERS OF TWO
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 22 March 2012, pp. 55-67
- Print publication:
- February 2013
-
- Article
-
- You have access
- Export citation
The L2 restriction norm of a GL3 Maass form
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 20 March 2012, pp. 675-717
- Print publication:
- May 2012
-
- Article
-
- You have access
- Export citation
Continued fractions with low complexity: transcendence measures and quadratic approximation
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 19 March 2012, pp. 718-750
- Print publication:
- May 2012
-
- Article
-
- You have access
- Export citation
Quantifying residual finiteness of arithmetic groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 19 March 2012, pp. 907-920
- Print publication:
- May 2012
-
- Article
-
- You have access
- Export citation
On numbers n dividing the nth term of a linear recurrence
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 23 February 2012, pp. 271-289
-
- Article
-
- You have access
- Export citation
ON A CONJECTURE OF ERDŐS
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 2 / July 2012
- Published online by Cambridge University Press:
- 23 February 2012, pp. 275-289
- Print publication:
- July 2012
-
- Article
- Export citation
On the convergence of Diophantine Dirichlet series
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 23 February 2012, pp. 513-541
-
- Article
-
- You have access
- Export citation
Local spectral equidistribution for Siegel modular forms and applications
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 2 / March 2012
- Published online by Cambridge University Press:
- 21 February 2012, pp. 335-384
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
ON THE EXPONENTIAL DIOPHANTINE EQUATION x2+p2m=2yn
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 2 / October 2012
- Published online by Cambridge University Press:
- 21 February 2012, pp. 303-314
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
ON ODD PERFECT NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 16 February 2012, pp. 510-514
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
ON THE DISTRIBUTION OF TORSION POINTS MODULO PRIMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 2 / October 2012
- Published online by Cambridge University Press:
- 16 February 2012, pp. 339-347
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
ON THE DIOPHANTINE EQUATION (8n)x+(15n)y=(17n)z
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 2 / October 2012
- Published online by Cambridge University Press:
- 07 February 2012, pp. 348-352
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
INFINITUDE OF ELLIPTIC CARMICHAEL NUMBERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 25 April 2012, pp. 45-60
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
EXPONENTIAL AND CHARACTER SUMS WITH MERSENNE NUMBERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 26 April 2012, pp. 1-13
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
RATIONAL APPROXIMATIONS TO VALUES OF BELL POLYNOMIALS AT POINTS INVOLVING EULER’S CONSTANT AND ZETA VALUES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 15 June 2012, pp. 71-98
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
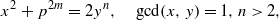
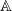 be a commutative algebraic group defined over a number field
be a commutative algebraic group defined over a number field  , we determine the average values of
, we determine the average values of