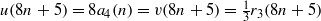Refine listing
Actions for selected content:
2818 results in 11xxx
ON THE RANKIN–SELBERG ZETA FUNCTION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 19 September 2012, pp. 101-113
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
On arithmetic families of filtered
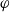 $\varphi $-modules and crystalline representations
$\varphi $-modules and crystalline representations
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 12 / Issue 4 / October 2013
- Published online by Cambridge University Press:
- 19 September 2012, pp. 677-726
- Print publication:
- October 2013
-
- Article
- Export citation
ON DIVISIBILITY OF BINOMIAL COEFFICIENTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 19 September 2012, pp. 189-201
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
NOTE ON ODD MULTIPERFECT NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 17 September 2012, pp. 448-451
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
THE RESONANCE METHOD FOR LARGE CHARACTER SUMS
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 11 September 2012, pp. 87-118
- Print publication:
- January 2013
-
- Article
- Export citation
Identifying supersingular elliptic curves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 September 2012, pp. 317-325
-
- Article
-
- You have access
- Export citation
On the use of expansion series for stream ciphers
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 September 2012, pp. 326-340
-
- Article
-
- You have access
- Export citation
Galois groups of chromatic polynomials
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 September 2012, pp. 281-307
-
- Article
-
- You have access
- Export citation
Complete addition laws on abelian varieties
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 September 2012, pp. 308-316
-
- Article
-
- You have access
- Export citation
ON MAHLER’S
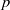 $p$-ADIC
$p$-ADIC 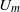 $U_{m}$-NUMBERS
$U_{m}$-NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 21 August 2012, pp. 44-50
- Print publication:
- August 2013
-
- Article
-
- You have access
- Export citation
THE MONTGOMERY–HOOLEY THEOREM IN SHORT INTERVALS
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 02 August 2012, pp. 129-139
- Print publication:
- January 2013
-
- Article
- Export citation
SOME OBSERVATIONS ON THE DIOPHANTINE EQUATION y2=x!+A AND RELATED RESULTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 02 August 2012, pp. 377-388
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
Accelerating the CM method
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 August 2012, pp. 172-204
-
- Article
-
- You have access
- Export citation
Sato–Tate distributions and Galois endomorphism modules in genus 2
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 5 / September 2012
- Published online by Cambridge University Press:
- 25 July 2012, pp. 1390-1442
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
JOINT UNIVERSALITY OF HURWITZ ZETA-FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 2 / October 2012
- Published online by Cambridge University Press:
- 09 July 2012, pp. 232-243
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
Boundary behaviour of special cohomology classes arising from the Weil representation
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 12 / Issue 3 / July 2013
- Published online by Cambridge University Press:
- 03 July 2012, pp. 571-634
- Print publication:
- July 2013
-
- Article
- Export citation
SOME PROPERTIES OF A SEQUENCE ANALOGOUS TO EULER NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 12 June 2012, pp. 425-440
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
ON MULTIPLICATIVELY BADLY APPROXIMABLE NUMBERS
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 12 June 2012, pp. 31-55
- Print publication:
- January 2013
-
- Article
- Export citation
INFINITE FAMILIES OF ARITHMETIC IDENTITIES FOR 4-CORES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 07 June 2012, pp. 304-315
- Print publication:
- April 2013
-
- Article
-
- You have access
- Export citation
Descent obstructions and Brauer–Manin obstruction in positive characteristic
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 12 / Issue 3 / July 2013
- Published online by Cambridge University Press:
- 01 June 2012, pp. 545-551
- Print publication:
- July 2013
-
- Article
- Export citation
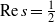
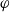
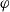
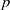
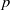
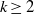
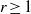
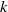

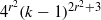
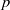
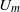
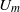
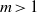
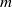
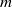
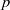
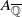 (the
(the 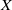
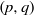
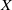
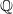
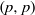
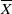
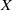
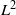
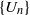
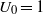
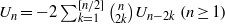
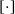
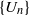
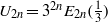
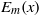
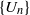
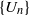
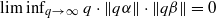 for all (
for all (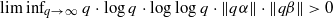 is of full dimension.
is of full dimension.