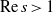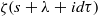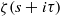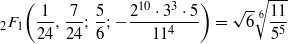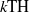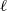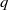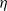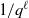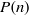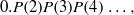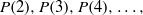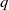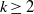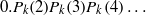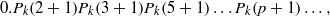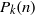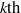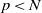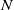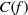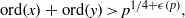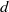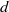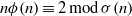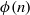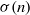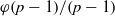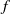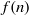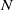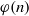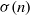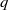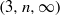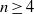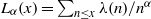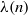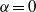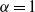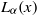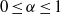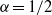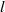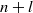Refine listing
Actions for selected content:
2818 results in 11xxx
SELF-APPROXIMATION FOR THE RIEMANN ZETA FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 31 October 2012, pp. 452-461
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
Representations of metaplectic groups I: epsilon dichotomy and local Langlands correspondence
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 6 / November 2012
- Published online by Cambridge University Press:
- 31 October 2012, pp. 1655-1694
- Print publication:
- November 2012
-
- Article
-
- You have access
- Export citation
Schwarzian differential equations and Hecke eigenforms on Shimura curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 31 October 2012, pp. 1-31
- Print publication:
- January 2013
-
- Article
- Export citation
CONSTRUCTION OF NORMAL NUMBERS USING THE DISTRIBUTION OF THE
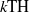 $k\rm TH$ LARGEST PRIME FACTOR
$k\rm TH$ LARGEST PRIME FACTOR
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 31 October 2012, pp. 158-168
- Print publication:
- August 2013
-
- Article
-
- You have access
- Export citation
ELEMENTS OF LARGE ORDER IN PRIME FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 16 October 2012, pp. 169-176
- Print publication:
- August 2013
-
- Article
-
- You have access
- Export citation
Critically separable rational maps in families
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 6 / November 2012
- Published online by Cambridge University Press:
- 12 October 2012, pp. 1880-1896
- Print publication:
- November 2012
-
- Article
-
- You have access
- Export citation
Lifting, restricting and sifting integral points on affine homogeneous varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 6 / November 2012
- Published online by Cambridge University Press:
- 11 October 2012, pp. 1695-1716
- Print publication:
- November 2012
-
- Article
-
- You have access
- Export citation
CLASSIFICATION AND SYMMETRIES OF A FAMILY OF CONTINUED FRACTIONS WITH BOUNDED PERIOD LENGTH
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 03 May 2013, pp. 53-76
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
APPROXIMATION OF AN ALGEBRAIC NUMBER BY PRODUCTS OF RATIONAL NUMBERS AND UNITS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 07 February 2013, pp. 121-131
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
COMPLEX NUMBERS WITH BOUNDED PARTIAL QUOTIENTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 16 April 2013, pp. 9-20
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
ON A VARIATION OF A CONGRUENCE OF SUBBARAO
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 04 February 2013, pp. 85-90
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
A NOTE ON THE DISTRIBUTION FUNCTION OF
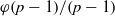 $ \varphi (\lowercase {P}-1)/(\lowercase {P}-1)$
$ \varphi (\lowercase {P}-1)/(\lowercase {P}-1)$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 16 January 2013, pp. 77-83
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
Efficient implementation of the Hardy–Ramanujan–Rademacher formula
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 October 2012, pp. 341-359
-
- Article
-
- You have access
- Export citation
WEAK PROPER DISTRIBUTION OF VALUES OF MULTIPLICATIVE FUNCTIONS IN RESIDUE CLASSES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 04 February 2013, pp. 173-188
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
ON THE OPTIMAL CONTINUED FRACTION EXPANSION OF A QUADRATIC SURD
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 07 February 2013, pp. 133-156
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
A VARIANT OF HOFSTADTER’S SEQUENCE AND FINITE AUTOMATA
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 03 May 2013, pp. 1-8
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
RELATIONS IN THE 2-CLASS GROUP OF QUADRATIC NUMBER FIELDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 07 February 2013, pp. 115-120
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
CONTINUED FRACTIONS FOR A CLASS OF TRIANGLE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 07 February 2013, pp. 21-42
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
BETWEEN THE PROBLEMS OF PÓLYA AND TURÁN
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 27 September 2012, pp. 157-171
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
TWIN SQUAREFUL NUMBERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 19 September 2012, pp. 43-51
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation