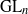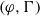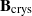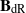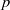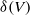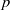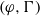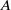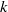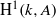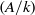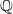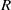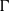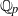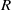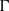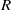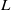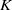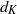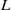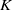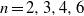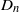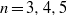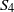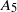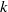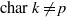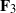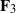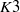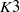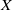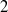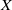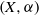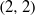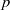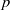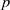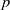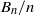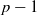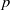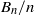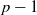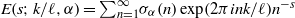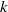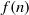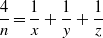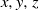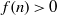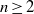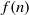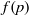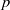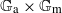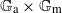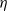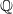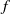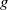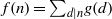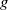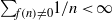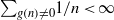Refine listing
Actions for selected content:
2818 results in 11xxx
Cusp eigenforms and the hall algebra of an elliptic curve
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 6 / June 2013
- Published online by Cambridge University Press:
- 04 March 2013, pp. 914-958
- Print publication:
- June 2013
-
- Article
- Export citation
Iwasawa theory of de Rham
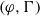 $(\varphi , \Gamma )$-modules over the Robba ring
$(\varphi , \Gamma )$-modules over the Robba ring
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 27 February 2013, pp. 65-118
- Print publication:
- January 2014
-
- Article
- Export citation
Weil–Châtelet divisible elements in Tate–Shafarevich groups I: The Bashmakov problem for elliptic curves over
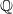 $ \mathbb{Q} $
$ \mathbb{Q} $
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 5 / May 2013
- Published online by Cambridge University Press:
- 26 February 2013, pp. 729-753
- Print publication:
- May 2013
-
- Article
- Export citation
On the Iwasawa theory of the Lubin–Tate moduli space
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 5 / May 2013
- Published online by Cambridge University Press:
- 26 February 2013, pp. 793-839
- Print publication:
- May 2013
-
- Article
- Export citation
Logarithmic derivatives of Artin
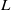 $L$-functions
$L$-functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 4 / April 2013
- Published online by Cambridge University Press:
- 26 February 2013, pp. 568-586
- Print publication:
- April 2013
-
- Article
- Export citation
THE VALUE DISTRIBUTION OF INCOMPLETE GAUSS SUMS
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 2 / July 2013
- Published online by Cambridge University Press:
- 19 February 2013, pp. 381-398
- Print publication:
- July 2013
-
- Article
- Export citation
JEŚMANOWICZ’ CONJECTURE REVISITED
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 15 February 2013, pp. 486-491
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
Computing zeta functions of nondegenerate hypersurfaces with few monomials
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 14 February 2013, pp. 9-44
-
- Article
-
- You have access
- Export citation
On admissible tensor products in p-adic Hodge theory
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 3 / March 2013
- Published online by Cambridge University Press:
- 14 February 2013, pp. 417-429
- Print publication:
- March 2013
-
- Article
- Export citation
The André–Oort conjecture for Drinfeld modular varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 4 / April 2013
- Published online by Cambridge University Press:
- 14 February 2013, pp. 507-567
- Print publication:
- April 2013
-
- Article
- Export citation
Random Dieudonné modules, random
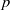 $p$-divisible groups, and random curves over finite fields
$p$-divisible groups, and random curves over finite fields
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 12 / Issue 3 / July 2013
- Published online by Cambridge University Press:
- 13 February 2013, pp. 651-676
- Print publication:
- July 2013
-
- Article
- Export citation
Failure of the Hasse principle on general
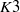 $K 3$ surfaces
$K 3$ surfaces
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 12 / Issue 4 / October 2013
- Published online by Cambridge University Press:
- 08 February 2013, pp. 853-877
- Print publication:
- October 2013
-
- Article
- Export citation
ON A CONJECTURE OF IGUSA
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 2 / July 2013
- Published online by Cambridge University Press:
- 07 February 2013, pp. 399-425
- Print publication:
- July 2013
-
- Article
- Export citation
THE UNIVERSAL KUMMER CONGRUENCES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 22 March 2013, pp. 106-132
- Print publication:
- February 2013
-
- Article
-
- You have access
- Export citation
ZEROS OF THE ESTERMANN ZETA FUNCTION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 01 March 2013, pp. 38-49
- Print publication:
- February 2013
-
- Article
-
- You have access
- Export citation
COUNTING THE NUMBER OF SOLUTIONS TO THE ERDŐS–STRAUS EQUATION ON UNIT FRACTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 15 May 2013, pp. 50-105
- Print publication:
- February 2013
-
- Article
-
- You have access
- Export citation
A SMALL VALUE ESTIMATE FOR
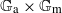 $\mathbb {G}_{{\textrm{a}}}\times \mathbb {G}_{{\textrm{m}}}$
$\mathbb {G}_{{\textrm{a}}}\times \mathbb {G}_{{\textrm{m}}}$
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 2 / July 2013
- Published online by Cambridge University Press:
- 01 February 2013, pp. 333-363
- Print publication:
- July 2013
-
- Article
- Export citation
UNCERTAINTY PRINCIPLES CONNECTED WITH THE MÖBIUS INVERSION FORMULA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 25 January 2013, pp. 460-472
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
A DIOPHANTINE PROBLEM CONCERNING POLYGONAL NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 25 January 2013, pp. 345-350
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
ZERO-ONE LAWS IN SIMULTANEOUS AND MULTIPLICATIVE DIOPHANTINE APPROXIMATION
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 2 / July 2013
- Published online by Cambridge University Press:
- 21 January 2013, pp. 321-332
- Print publication:
- July 2013
-
- Article
- Export citation