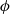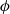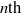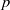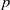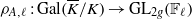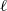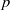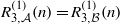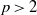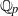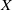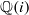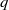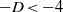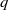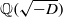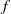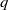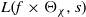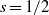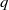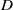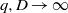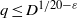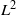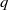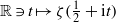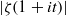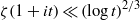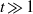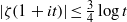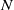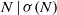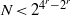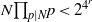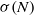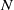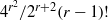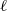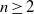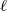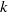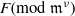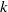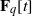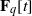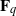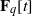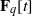Refine listing
Actions for selected content:
2818 results in 11xxx
Explicit application of Waldspurger’s theorem
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 August 2013, pp. 216-245
-
- Article
-
- You have access
- Export citation
Computing level one Hecke eigensystems (mod
 $p$ )
$p$ )
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 August 2013, pp. 246-270
-
- Article
-
- You have access
- Export citation
Modular subgroups, dessins d’enfants and elliptic K3 surfaces
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 August 2013, pp. 271-318
-
- Article
-
- You have access
- Export citation
Determinants of subquotients of Galois representations associated with abelian varieties
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 3 / July 2014
- Published online by Cambridge University Press:
- 18 July 2013, pp. 517-559
- Print publication:
- July 2014
-
- Article
- Export citation
Knots which behave like the prime numbers
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 8 / August 2013
- Published online by Cambridge University Press:
- 10 July 2013, pp. 1235-1244
- Print publication:
- August 2013
-
- Article
- Export citation
On the arithmetic fundamental lemma in the minuscule case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 10 / October 2013
- Published online by Cambridge University Press:
- 04 July 2013, pp. 1631-1666
- Print publication:
- October 2013
-
- Article
- Export citation
A removal lemma for linear configurations in subsets of the circle
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 3 / October 2013
- Published online by Cambridge University Press:
- 28 June 2013, pp. 657-666
-
- Article
-
- You have access
- Export citation
SETS WITH ALMOST COINCIDING REPRESENTATION FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 28 June 2013, pp. 97-111
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
ON WARING’S PROBLEM: TWO SQUARES AND THREE BIQUADRATES
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 28 June 2013, pp. 153-165
- Print publication:
- January 2014
-
- Article
- Export citation
A geometric perspective on the Breuil–Mézard conjecture
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 26 June 2013, pp. 183-223
- Print publication:
- January 2014
-
- Article
- Export citation
Rational points on singular intersections of quadrics
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 9 / September 2013
- Published online by Cambridge University Press:
- 20 June 2013, pp. 1457-1494
- Print publication:
- September 2013
-
- Article
- Export citation
Subconvexity and equidistribution of Heegner points in the level aspect
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 7 / July 2013
- Published online by Cambridge University Press:
- 17 June 2013, pp. 1150-1174
- Print publication:
- July 2013
-
- Article
- Export citation
NEGATIVE VALUES OF THE RIEMANN ZETA FUNCTION ON THE CRITICAL LINE
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 2 / July 2013
- Published online by Cambridge University Press:
- 17 June 2013, pp. 443-462
- Print publication:
- July 2013
-
- Article
- Export citation
A NEW UPPER BOUND FOR
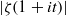 $\vert \zeta (1+ it)\vert $
$\vert \zeta (1+ it)\vert $
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 13 June 2013, pp. 259-264
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
SOLUTIONS TO POLYNOMIAL CONGRUENCES IN WELL-SHAPED SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 12 June 2013, pp. 435-447
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
IMPROVED UPPER BOUNDS FOR ODD MULTIPERFECT NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 12 June 2013, pp. 353-359
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
ADDITION TO ‘AN UPPER BOUND FOR THE NUMBER OF ODD MULTIPERFECT NUMBERS’
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 07 June 2013, pp. 5-7
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
Rationality problems and conjectures of Milnor and Bloch–Kato
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 8 / August 2013
- Published online by Cambridge University Press:
- 03 June 2013, pp. 1312-1326
- Print publication:
- August 2013
-
- Article
- Export citation
Complexity of OM factorizations of polynomials over local fields
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 June 2013, pp. 139-171
-
- Article
-
- You have access
- Export citation
REPRESENTING AN ELEMENT IN
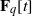 ${\mathbf{F} }_{q} [t] $ AS THE SUM OF TWO IRREDUCIBLES
${\mathbf{F} }_{q} [t] $ AS THE SUM OF TWO IRREDUCIBLES
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 23 May 2013, pp. 166-182
- Print publication:
- January 2014
-
- Article
- Export citation