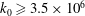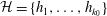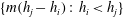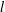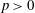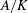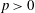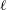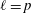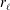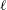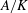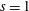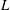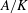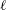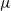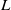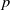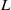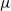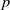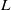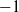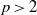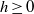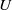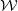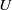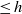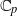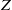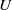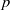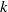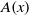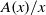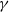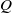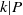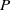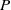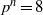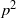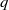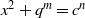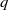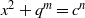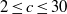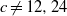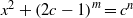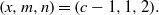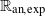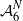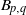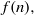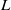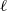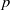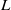Refine listing
Actions for selected content:
2818 results in 11xxx
On a completed generating function of locally harmonic Maass forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 5 / May 2014
- Published online by Cambridge University Press:
- 26 March 2014, pp. 749-762
- Print publication:
- May 2014
-
- Article
- Export citation
A NOTE ON THE POLIGNAC NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 13 March 2014, pp. 500-502
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
The
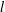 $l$-parity conjecture for abelian varieties over function fields of characteristic
$l$-parity conjecture for abelian varieties over function fields of characteristic 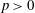 $p>0$
$p>0$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 4 / April 2014
- Published online by Cambridge University Press:
- 10 March 2014, pp. 507-522
- Print publication:
- April 2014
-
- Article
- Export citation
Random Construction of Interpolating Sets for High-Dimensional Integration
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 1 / March 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 92-105
- Print publication:
- March 2014
-
- Article
-
- You have access
- Export citation
On the
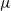 $\mu $ -invariant of the cyclotomic derivative of a Katz p-adic
$\mu $ -invariant of the cyclotomic derivative of a Katz p-adic 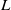 $L$ -function
$L$ -function
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 10 January 2014, pp. 131-148
- Print publication:
- January 2015
-
- Article
- Export citation
COUNTING SYMMETRIC COLOURINGS OF THE VERTICES OF A REGULAR POLYGON
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 10 January 2014, pp. 1-8
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
Overconvergent Eichler–Shimura isomorphisms
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 02 January 2014, pp. 221-274
- Print publication:
- April 2015
-
- Article
- Export citation
THE ERROR TERM IN THE COUNT OF ABUNDANT NUMBERS
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 02 January 2014, pp. 43-65
- Print publication:
- January 2014
-
- Article
- Export citation
CONVEX CURVES AND A POISSON IMITATION OF LATTICES
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 02 January 2014, pp. 139-152
- Print publication:
- January 2014
-
- Article
- Export citation
THE SQUARE TERMS IN GENERALIZED LUCAS SEQUENCES
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 19 December 2013, pp. 85-100
- Print publication:
- January 2014
-
- Article
- Export citation
POLYNOMIAL EQUIVALENCE OF FINITE RINGS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 244-257
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
Galois representations associated to holomorphic limits of discrete series
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 2 / February 2014
- Published online by Cambridge University Press:
- 26 November 2013, pp. 191-228
- Print publication:
- February 2014
-
- Article
- Export citation
A NOTE ON THE DIOPHANTINE EQUATION
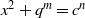 ${x}^{2} + {q}^{m} = {c}^{n} $
${x}^{2} + {q}^{m} = {c}^{n} $
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 26 November 2013, pp. 20-27
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
Applications du théorème d’Ax–Lindemann hyperbolique
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 2 / February 2014
- Published online by Cambridge University Press:
- 19 November 2013, pp. 175-190
- Print publication:
- February 2014
-
- Article
- Export citation
Singular values of multiple eta-quotients for ramified primes
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 07 November 2013, pp. 407-418
-
- Article
-
- You have access
- Export citation
SPECIAL POINT PROBLEMS WITH ELLIPTIC MODULAR SURFACES
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 06 November 2013, pp. 1-31
- Print publication:
- January 2014
-
- Article
- Export citation
LENS SPACE SURGERIES ALONG CERTAIN 2-COMPONENT LINKS RELATED WITH PARK’S RATIONAL BLOW DOWN, AND REIDEMEISTER-TURAEV TORSION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 15 October 2013, pp. 78-126
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
Comptage des
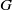 $G$-chtoucas: la partie elliptique
$G$-chtoucas: la partie elliptique
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 12 / December 2013
- Published online by Cambridge University Press:
- 07 October 2013, pp. 2169-2183
- Print publication:
- December 2013
-
- Article
- Export citation
ARITHMETIC PROPERTIES OF 1-SHELL TOTALLY SYMMETRIC PLANE PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 27 September 2013, pp. 473-478
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
Trivial zeros of
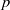 $p$ -adic
$p$ -adic 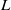 $L$ -functions at near-central points
$L$ -functions at near-central points
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 3 / July 2014
- Published online by Cambridge University Press:
- 24 September 2013, pp. 561-598
- Print publication:
- July 2014
-
- Article
- Export citation