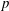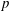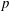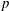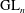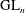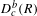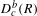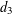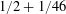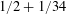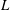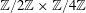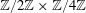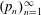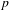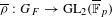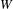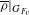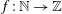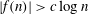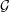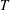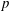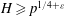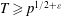Refine listing
Actions for selected content:
2818 results in 11xxx
Modularity of nearly ordinary 2-adic residually dihedral Galois representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 8 / August 2014
- Published online by Cambridge University Press:
- 16 June 2014, pp. 1235-1346
- Print publication:
- August 2014
-
- Article
- Export citation
The
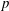 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$-cyclic McKay correspondence via motivic integration
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$-cyclic McKay correspondence via motivic integration
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 7 / July 2014
- Published online by Cambridge University Press:
- 10 June 2014, pp. 1125-1168
- Print publication:
- July 2014
-
- Article
- Export citation
Raising the level for
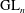 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\text {GL}_{{n}}$
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\text {GL}_{{n}}$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 10 June 2014, e16
-
- Article
-
- You have access
- Open access
- Export citation
RATIONAL POINTS ON INTERSECTIONS OF CUBIC AND QUADRIC HYPERSURFACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 4 / October 2015
- Published online by Cambridge University Press:
- 05 June 2014, pp. 703-749
- Print publication:
- October 2015
-
- Article
- Export citation
THE p-COHOMOLOGY OF ALGEBRAIC VARIETIES AND SPECIAL VALUES OF ZETA FUNCTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 4 / October 2015
- Published online by Cambridge University Press:
- 02 June 2014, pp. 801-835
- Print publication:
- October 2015
-
- Article
- Export citation
ON THE EXPONENT OF DISTRIBUTION OF THE TERNARY DIVISOR FUNCTION
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 02 June 2014, pp. 121-144
- Print publication:
- January 2015
-
- Article
- Export citation
Evaluating
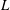 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}L$ -functions with few known coefficients
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}L$ -functions with few known coefficients
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 June 2014, pp. 245-258
-
- Article
-
- You have access
- Export citation
High-rank elliptic curves with torsion
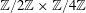 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Z}/2\mathbb{Z}\times \mathbb{Z}/4\mathbb{Z}$ induced by Diophantine triples
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Z}/2\mathbb{Z}\times \mathbb{Z}/4\mathbb{Z}$ induced by Diophantine triples
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 June 2014, pp. 282-288
-
- Article
-
- You have access
- Export citation
FROM SEPARABLE POLYNOMIALS TO NONEXISTENCE OF RATIONAL POINTS ON CERTAIN HYPERELLIPTIC CURVES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 16 June 2014, pp. 354-385
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
On the beta expansion of Salem numbers of degree 8
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 June 2014, pp. 289-301
-
- Article
-
- You have access
- Export citation
A FAMILY OF MULTIPLE HARMONIC SUM AND MULTIPLE ZETA STAR VALUE IDENTITIES
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 28 May 2014, pp. 63-71
- Print publication:
- January 2015
-
- Article
- Export citation
ON THE METRIC THEORY OF CONTINUED FRACTIONS IN POSITIVE CHARACTERISTIC
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 2 / July 2014
- Published online by Cambridge University Press:
- 27 May 2014, pp. 307-320
- Print publication:
- July 2014
-
- Article
-
- You have access
- Export citation
MULTIPLE EXPONENTIAL AND CHARACTER SUMS WITH MONOMIALS
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 2 / July 2014
- Published online by Cambridge University Press:
- 27 May 2014, pp. 363-373
- Print publication:
- July 2014
-
- Article
- Export citation
ON CHARACTERIZATION OF SIEGEL CUSP FORMS OF DEGREE 2 BY THE HECKE BOUND
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 27 May 2014, pp. 89-100
- Print publication:
- January 2015
-
- Article
- Export citation
SERRE WEIGHTS FOR LOCALLY REDUCIBLE TWO-DIMENSIONAL GALOIS REPRESENTATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 3 / July 2015
- Published online by Cambridge University Press:
- 23 May 2014, pp. 639-672
- Print publication:
- July 2015
-
- Article
- Export citation
ON DEFICIENT-PERFECT NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 23 May 2014, pp. 186-194
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
THE MINIMAL GROWTH OF A
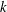 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}k$-REGULAR SEQUENCE
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}k$-REGULAR SEQUENCE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 22 May 2014, pp. 195-203
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
GENERALISATION OF KEITH’S CONJECTURE ON 9-REGULAR PARTITIONS AND 3-CORES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 20 May 2014, pp. 204-212
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
Double Character Sums over Subgroups and Intervals
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 15 May 2014, pp. 376-390
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
A NOTE ON INTERPOLATION OF PERMUTATIONS OF A SUBSET OF A FINITE FIELD
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 15 May 2014, pp. 213-219
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation