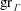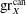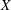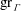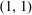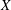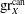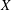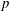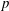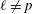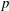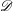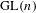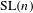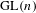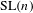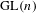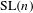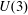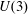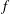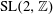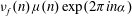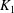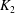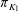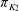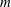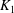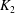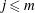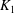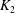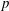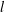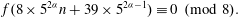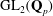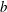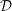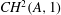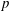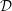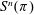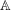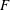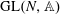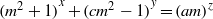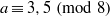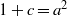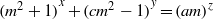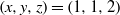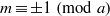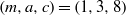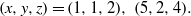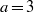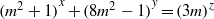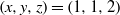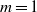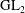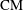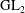Refine listing
Actions for selected content:
2818 results in 11xxx
EXPLICIT BOUNDS ON AUTOMORPHIC AND CANONICAL GREEN FUNCTIONS OF FUCHSIAN GROUPS
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 2 / July 2014
- Published online by Cambridge University Press:
- 14 May 2014, pp. 257-306
- Print publication:
- July 2014
-
- Article
- Export citation
Product formula for p -adic epsilon factors
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 08 May 2014, pp. 275-377
- Print publication:
- April 2015
-
- Article
- Export citation
LIMIT MULTIPLICITIES FOR PRINCIPAL CONGRUENCE SUBGROUPS OF
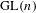 $\text{GL}(n)$ AND
$\text{GL}(n)$ AND 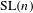 $\text{SL}(n)$
$\text{SL}(n)$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 3 / July 2015
- Published online by Cambridge University Press:
- 08 May 2014, pp. 589-638
- Print publication:
- July 2015
-
- Article
- Export citation
Computation of Galois groups of rational polynomials
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 May 2014, pp. 141-158
-
- Article
-
- You have access
- Export citation
Endoscopy and cohomology growth on
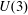 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}U(3)$
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}U(3)$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 6 / June 2014
- Published online by Cambridge University Press:
- 24 April 2014, pp. 903-910
- Print publication:
- June 2014
-
- Article
- Export citation
Strong orthogonality between the Möbius function, additive characters and Fourier coefficients of cusp forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 5 / May 2014
- Published online by Cambridge University Press:
- 24 April 2014, pp. 763-797
- Print publication:
- May 2014
-
- Article
- Export citation
THE QUANTITATIVE DISTRIBUTION OF HECKE EIGENVALUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 10 April 2014, pp. 28-36
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
AN EFFICIENT METHOD FOR IMPROVING THE COMPUTATIONAL PERFORMANCE OF THE CUBIC LUCAS CRYPTOSYSTEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 10 April 2014, pp. 160-171
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
Ramification theory and perfectoid spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 5 / May 2014
- Published online by Cambridge University Press:
- 03 April 2014, pp. 798-834
- Print publication:
- May 2014
-
- Article
- Export citation
NEW INFINITE FAMILIES OF CONGRUENCES MODULO 4 AND 8 FOR 1-SHELL TOTALLY SYMMETRIC PLANE PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 02 April 2014, pp. 37-46
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
Computing fundamental domains for the Bruhat–Tits tree for
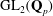 ${\rm GL}_2(\mathbf{Q}_p)$ ,
${\rm GL}_2(\mathbf{Q}_p)$ , 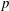 $p$ -adic automorphic forms, and the canonical embedding of Shimura curves
$p$ -adic automorphic forms, and the canonical embedding of Shimura curves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 1-23
-
- Article
-
- You have access
- Export citation
On a conjecture of Rudin on squares in arithmetic progressions
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 58-76
-
- Article
-
- You have access
- Export citation
Wieferich pairs and Barker sequences, II
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 24-32
-
- Article
-
- You have access
- Export citation
THE INTERSECTION OF PIATETSKI-SHAPIRO SEQUENCES
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 2 / July 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 347-362
- Print publication:
- July 2014
-
- Article
- Export citation
THE TILED CIRCLE PROBLEM
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 2 / July 2014
- Published online by Cambridge University Press:
- 31 March 2014, pp. 321-346
- Print publication:
- July 2014
-
- Article
- Export citation
AN ARITHMETICAL EXCURSION VIA STONEHAM NUMBERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 27 March 2014, pp. 303-315
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
Higher Chow cycles on Abelian surfaces and a non-Archimedean analogue of the Hodge-
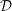 ${\mathcal{D}}$-conjecture
${\mathcal{D}}$-conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 4 / April 2014
- Published online by Cambridge University Press:
- 26 March 2014, pp. 691-711
- Print publication:
- April 2014
-
- Article
- Export citation
Level-raising and symmetric power functoriality, I
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 5 / May 2014
- Published online by Cambridge University Press:
- 26 March 2014, pp. 729-748
- Print publication:
- May 2014
-
- Article
- Export citation
ON THE EXPONENTIAL DIOPHANTINE EQUATION
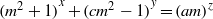 $\mathop{({m}^{2} + 1)}\nolimits ^{x} + \mathop{(c{m}^{2} - 1)}\nolimits ^{y} = \mathop{(am)}\nolimits ^{z} $
$\mathop{({m}^{2} + 1)}\nolimits ^{x} + \mathop{(c{m}^{2} - 1)}\nolimits ^{y} = \mathop{(am)}\nolimits ^{z} $
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 26 March 2014, pp. 9-19
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
Galois representations attached to automorphic forms on
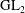 ${\rm GL}_2$ over
${\rm GL}_2$ over 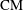 ${\rm CM}$ fields
${\rm CM}$ fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 4 / April 2014
- Published online by Cambridge University Press:
- 26 March 2014, pp. 523-567
- Print publication:
- April 2014
-
- Article
- Export citation