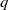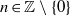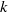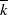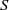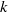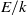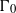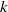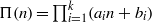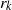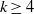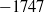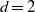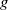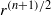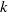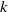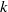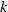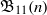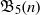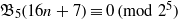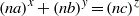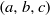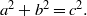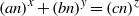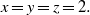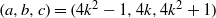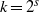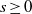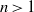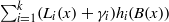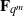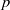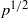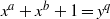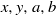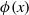Refine listing
Actions for selected content:
2818 results in 11xxx
MOCK THETA FUNCTIONS AND QUANTUM MODULAR FORMS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 1 / 2013
- Published online by Cambridge University Press:
- 19 September 2013, e2
-
- Article
-
- You have access
- Open access
- Export citation
SPECIAL CURVES AND POSTCRITICALLY FINITE POLYNOMIALS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 1 / 2013
- Published online by Cambridge University Press:
- 19 September 2013, e3
-
- Article
-
- You have access
- Open access
- Export citation
VARIATIONS ON A THEOREM OF DAVENPORT CONCERNING ABUNDANT NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 12 September 2013, pp. 437-450
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
UNIQUE REPRESENTATION BI-BASIS FOR THE INTEGERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 12 September 2013, pp. 460-465
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
ON THE INTEGRAL HODGE AND TATE CONJECTURES OVER A NUMBER FIELD
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 1 / 2013
- Published online by Cambridge University Press:
- 12 September 2013, e4
-
- Article
-
- You have access
- Open access
- Export citation
Integral division points on curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 12 / December 2013
- Published online by Cambridge University Press:
- 09 September 2013, pp. 2011-2035
- Print publication:
- December 2013
-
- Article
- Export citation
ALMOST-PRIME
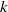 $k$-TUPLES
$k$-TUPLES
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 06 September 2013, pp. 108-138
- Print publication:
- January 2014
-
- Article
- Export citation
COUNTING RATIONAL POINTS ON CUBIC HYPERSURFACES: CORRIGENDUM
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 06 September 2013, pp. 101-107
- Print publication:
- January 2014
-
- Article
-
- You have access
- Export citation
On the Kohnen plus space for Hilbert modular forms of half-integral weight I
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 12 / December 2013
- Published online by Cambridge University Press:
- 06 September 2013, pp. 1963-2010
- Print publication:
- December 2013
-
- Article
- Export citation
Higher torsion in the Abelianization of the full Bianchi groups
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 September 2013, pp. 344-365
-
- Article
-
- You have access
- Export citation
MIXING FOR PROGRESSIONS IN NONABELIAN GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 1 / 2013
- Published online by Cambridge University Press:
- 29 August 2013, e2
-
- Article
-
- You have access
- Open access
- Export citation
COUNTING SYMMETRIC BRACELETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 22 August 2013, pp. 431-436
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
CONGRUENCES MODULO POWERS OF 2 FOR FU’S 5 DOTS BRACELET PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 22 August 2013, pp. 360-372
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
A NOTE ON THE DIOPHANTINE EQUATION
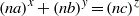 $\mathop{(na)}\nolimits ^{x} + \mathop{(nb)}\nolimits ^{y} = \mathop{(nc)}\nolimits ^{z} $
$\mathop{(na)}\nolimits ^{x} + \mathop{(nb)}\nolimits ^{y} = \mathop{(nc)}\nolimits ^{z} $
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 07 August 2013, pp. 316-321
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
CONSTRUCTING PERMUTATION POLYNOMIALS OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 07 August 2013, pp. 420-430
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
ON SOLUTIONS TO SOME POLYNOMIAL CONGRUENCES IN SMALL BOXES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 07 August 2013, pp. 300-307
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
PERFECT POWERS WITH THREE DIGITS
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 06 August 2013, pp. 66-84
- Print publication:
- January 2014
-
- Article
- Export citation
Computing Borcherds products
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 August 2013, pp. 200-215
-
- Article
-
- You have access
- Export citation
On level one cuspidal Bianchi modular forms
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 August 2013, pp. 187-199
-
- Article
-
- You have access
- Export citation
Single-class genera of positive integral lattices
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 August 2013, pp. 172-186
-
- Article
-
- You have access
- Export citation