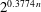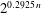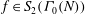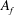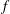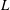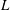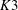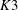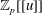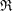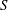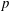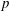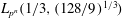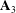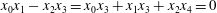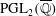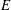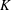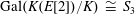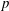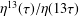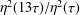Refine listing
Actions for selected content:
2818 results in 11xxx
A sieve algorithm based on overlattices
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 49-70
-
- Article
-
- You have access
- Export citation
Minimal models for
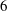 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}6$-coverings of elliptic curves
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}6$-coverings of elliptic curves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 112-127
-
- Article
-
- You have access
- Export citation
Computing Hasse–Witt matrices of hyperelliptic curves in average polynomial time
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 257-273
-
- Article
-
- You have access
- Export citation
Computation of Mordell–Weil bases for ordinary elliptic curves in characteristic two
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 1-13
-
- Article
-
- You have access
- Export citation
Computing Galois representations of modular abelian surfaces
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 36-48
-
- Article
-
- You have access
- Export citation
Hyper-and-elliptic-curve cryptography
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 181-202
-
- Article
-
- You have access
- Export citation
Nonvanishing of twists of
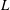 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}L$-functions attached to Hilbert modular forms
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}L$-functions attached to Hilbert modular forms
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 330-348
-
- Article
-
- You have access
- Export citation
Examples of
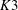 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}K3$ surfaces with real multiplication
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}K3$ surfaces with real multiplication
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 14-35
-
- Article
-
- You have access
- Export citation
Linear algebra over
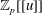 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Z}_p[[u]]$ and related rings
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Z}_p[[u]]$ and related rings
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 302-344
-
- Article
-
- You have access
- Export citation
Computing in quotients of rings of integers
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 349-365
-
- Article
-
- You have access
- Export citation
The multiple number field sieve for medium- and high-characteristic finite fields
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 230-246
-
- Article
-
- You have access
- Export citation
Counting imaginary quadratic points via universal torsors
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 10 / October 2014
- Published online by Cambridge University Press:
- 25 July 2014, pp. 1631-1678
- Print publication:
- October 2014
-
- Article
- Export citation
Corrigendum: Elliptic curves with a given number of points over finite fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 8 / August 2014
- Published online by Cambridge University Press:
- 17 July 2014, pp. 1347-1348
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
Modularity lifting results in parallel weight one and applications to the Artin conjecture: the tamely ramified case
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 10 July 2014, e18
-
- Article
-
- You have access
- Open access
- Export citation
ON A VARIANT OF A QUESTION PROPOSED BY K. MAHLER CONCERNING LIOUVILLE NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 09 July 2014, pp. 29-33
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
RAMANUJAN SERIES UPSIDE-DOWN
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 07 July 2014, pp. 78-106
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
A census of quadratic post-critically finite rational functions defined over
 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Q}$
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Q}$
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 July 2014, pp. 314-329
-
- Article
-
- You have access
- Export citation
A Markov model for Selmer ranks in families of twists
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 7 / July 2014
- Published online by Cambridge University Press:
- 30 June 2014, pp. 1077-1106
- Print publication:
- July 2014
-
- Article
- Export citation
EISENSTEIN SERIES TO THE TREDECIC BASE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 27 June 2014, pp. 19-28
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
Metric Diophantine approximation on homogeneous varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 8 / August 2014
- Published online by Cambridge University Press:
- 20 June 2014, pp. 1435-1456
- Print publication:
- August 2014
-
- Article
- Export citation