Refine listing
Actions for selected content:
2818 results in 11xxx
ADVENTURES IN INVARIANT THEORY
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 56 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 15 December 2014, pp. 105-115
-
- Article
-
- You have access
- Export citation
THE NUMBER OF SOLUTIONS TO MORDELL’S EQUATION IN CONSTRAINED RANGES
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 05 December 2014, pp. 708-718
- Print publication:
- September 2015
-
- Article
- Export citation
Group schemes and local densities of quadratic lattices in residue characteristic 2
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 5 / May 2015
- Published online by Cambridge University Press:
- 05 December 2014, pp. 793-827
- Print publication:
- May 2015
-
- Article
- Export citation
ALMOST-PRIME VALUES OF BINARY FORMS WITH ONE PRIME VARIABLE
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 05 December 2014, pp. 741-755
- Print publication:
- September 2015
-
- Article
- Export citation
A database of number fields
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 December 2014, pp. 595-618
-
- Article
-
- You have access
- Export citation
Level 1 Hecke algebras of modular forms modulo
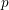 $p$
$p$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 3 / March 2015
- Published online by Cambridge University Press:
- 27 November 2014, pp. 397-415
- Print publication:
- March 2015
-
- Article
- Export citation
On the anticyclotomic Iwasawa main conjecture for modular forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 5 / May 2015
- Published online by Cambridge University Press:
- 27 November 2014, pp. 863-897
- Print publication:
- May 2015
-
- Article
- Export citation
LOCAL INTERDEFINABILITY OF WEIERSTRASS ELLIPTIC FUNCTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 4 / October 2016
- Published online by Cambridge University Press:
- 24 November 2014, pp. 673-691
- Print publication:
- October 2016
-
- Article
- Export citation
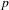 $p$-ADIC EISENSTEIN SERIES AND
$p$-ADIC EISENSTEIN SERIES AND  $L$-FUNCTIONS OF CERTAIN CUSP FORMS ON DEFINITE UNITARY GROUPS
$L$-FUNCTIONS OF CERTAIN CUSP FORMS ON DEFINITE UNITARY GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 3 / July 2016
- Published online by Cambridge University Press:
- 21 November 2014, pp. 471-510
- Print publication:
- July 2016
-
- Article
- Export citation
THE CATENARY DEGREE OF KRULL MONOIDS II
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 21 November 2014, pp. 324-354
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
Periods of automorphic forms: the case of
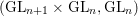 $(\text{GL}_{n+1}\times \text{GL}_{n},\text{GL}_{n})$
$(\text{GL}_{n+1}\times \text{GL}_{n},\text{GL}_{n})$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 4 / April 2015
- Published online by Cambridge University Press:
- 13 November 2014, pp. 665-712
- Print publication:
- April 2015
-
- Article
- Export citation
Big Galois representations and
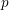 $p$-adic
$p$-adic 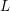 $L$-functions
$L$-functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 4 / April 2015
- Published online by Cambridge University Press:
- 13 November 2014, pp. 603-664
- Print publication:
- April 2015
-
- Article
- Export citation
Selmer groups and class groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 3 / March 2015
- Published online by Cambridge University Press:
- 11 November 2014, pp. 416-434
- Print publication:
- March 2015
-
- Article
- Export citation
ALGEBRAIC INDEPENDENCE OF CERTAIN MAHLER FUNCTIONS AND OF THEIR VALUES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 11 November 2014, pp. 289-310
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
FURTHER RESULTS ON VANISHING COEFFICIENTS IN INFINITE PRODUCT EXPANSIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 11 November 2014, pp. 69-77
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
ON POSITIVE PROPORTION OF RANK-ZERO TWISTS OF ELLIPTIC CURVES OVER
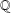 $\mathbb{Q}$
$\mathbb{Q}$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 07 November 2014, pp. 281-288
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
AN
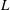 $L$ -FUNCTION-FREE PROOF OF VINOGRADOV’S THREE PRIMES THEOREM
$L$ -FUNCTION-FREE PROOF OF VINOGRADOV’S THREE PRIMES THEOREM
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 04 November 2014, e27
-
- Article
-
- You have access
- Open access
- Export citation
A classification of all 1-Salem graphs
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 November 2014, pp. 582-594
-
- Article
-
- You have access
- Export citation
A Frostman-Type Lemma for Sets with Large Intersections, and an Application to Diophantine Approximation
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 27 October 2014, pp. 521-542
-
- Article
-
- You have access
- Export citation
Equivariant Compactifications of Two-Dimensional Algebraic Groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 27 October 2014, pp. 149-168
-
- Article
-
- You have access
- Export citation
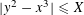
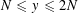
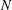
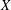
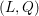
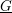
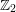
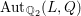
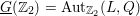
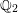
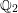
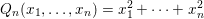
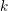
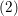
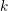
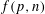
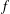
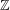
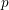
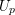
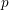
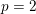
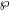
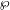
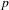

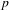

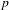
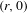

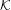
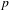
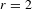
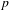

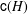
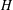
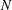
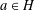
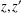

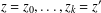

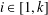
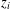
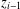
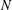
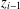
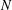
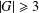
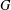
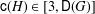
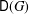
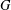
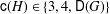
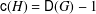
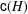
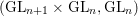
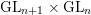
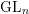
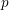
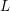
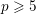
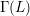
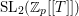
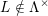
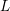
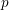
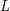
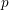
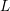

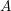
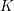
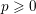
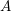
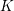
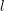
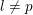
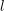
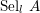
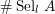
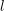
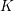
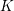
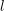
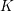
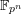
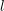
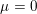
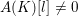
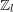
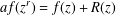


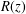
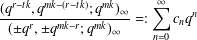


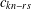
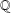
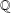
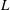
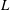
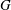
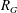
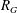
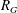
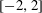
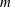
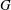
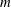
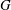
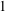
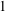
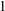
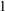
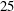
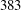
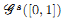 of subsets of [0, 1], originally introduced by Falconer, that are closed under countable intersections, and such that every set in the class has Hausdorff dimension at least
of subsets of [0, 1], originally introduced by Falconer, that are closed under countable intersections, and such that every set in the class has Hausdorff dimension at least 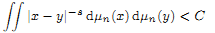
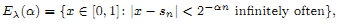
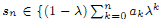 and
and 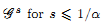 . This improves one of our previously published results.
. This improves one of our previously published results.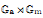 on ℙ
on ℙ