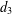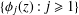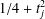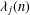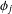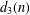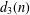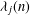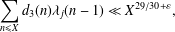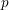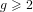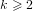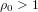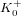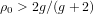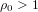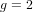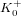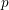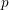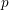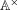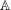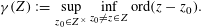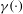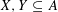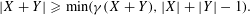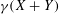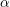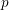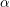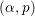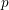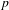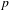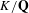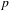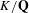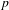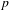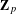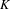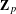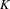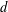Refine listing
Actions for selected content:
2818 results in 11xxx
Le complémentaire des puissances
 $n$-ièmes dans un corps de nombres est un ensemble diophantien
$n$-ièmes dans un corps de nombres est un ensemble diophantien
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 10 / October 2015
- Published online by Cambridge University Press:
- 22 June 2015, pp. 1965-1980
- Print publication:
- October 2015
-
- Article
- Export citation
SOME QUARTIC DIOPHANTINE EQUATIONS IN THE GAUSSIAN INTEGERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 16 June 2015, pp. 187-194
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
ON THE CENTRE OF THE AUTOMORPHISM GROUP OF A GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 16 June 2015, pp. 390-396
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
SPECIAL VALUES OF SHIFTED CONVOLUTION DIRICHLET SERIES
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 16 June 2015, pp. 47-66
- Print publication:
- 2016
-
- Article
- Export citation
THE MOONSHINE MODULE FOR CONWAY’S GROUP
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 3 / 2015
- Published online by Cambridge University Press:
- 15 June 2015, e10
-
- Article
-
- You have access
- Open access
- Export citation
Mutations of Fake Weighted Projective Planes
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 10 June 2015, pp. 271-285
-
- Article
- Export citation
On p-adic analytic continuation with applications to generating elements
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 10 June 2015, pp. 1-10
-
- Article
- Export citation
Groups generated by iterations of polynomials over finite fields
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 05 June 2015, pp. 235-245
-
- Article
- Export citation
Some applications of modular units
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 03 June 2015, pp. 91-106
-
- Article
- Export citation
SHIFTED CONVOLUTION SUM OF
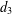 $d_{3}$ AND THE FOURIER COEFFICIENT OF HECKE–MAASS FORMS
$d_{3}$ AND THE FOURIER COEFFICIENT OF HECKE–MAASS FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 02 June 2015, pp. 195-204
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
SHRINKING TARGETS FOR NONAUTONOMOUS DYNAMICAL SYSTEMS CORRESPONDING TO CANTOR SERIES EXPANSIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 02 June 2015, pp. 205-213
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
Beyond endoscopy via the trace formula: 1. Poisson summation and isolation of special representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 10 / October 2015
- Published online by Cambridge University Press:
- 01 June 2015, pp. 1791-1820
- Print publication:
- October 2015
-
- Article
- Export citation
On the smooth transfer for Guo–Jacquet relative trace formulae
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 10 / October 2015
- Published online by Cambridge University Press:
- 01 June 2015, pp. 1821-1877
- Print publication:
- October 2015
-
- Article
- Export citation
Rational points on linear slices of diagonal hypersurfaces
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 218 / June 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 51-100
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
Heuristics on pairing-friendly abelian varieties
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 June 2015, pp. 419-443
-
- Article
-
- You have access
- Export citation
Hecke characters associated to Drinfeld modular forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 11 / November 2015
- Published online by Cambridge University Press:
- 01 June 2015, pp. 2006-2058
- Print publication:
- November 2015
-
- Article
- Export citation
CAUCHY–DAVENPORT TYPE THEOREMS FOR SEMIGROUPS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 22 May 2015, pp. 1-12
- Print publication:
- 2016
-
- Article
- Export citation
On the complexity of a putative counterexample to the
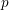 $p$-adic Littlewood conjecture
$p$-adic Littlewood conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 9 / September 2015
- Published online by Cambridge University Press:
- 19 May 2015, pp. 1647-1662
- Print publication:
- September 2015
-
- Article
- Export citation
ON THE NON-TRIVIALITY OF THE
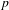 $p$ -ADIC ABEL–JACOBI IMAGE OF GENERALISED HEEGNER CYCLES MODULO
$p$ -ADIC ABEL–JACOBI IMAGE OF GENERALISED HEEGNER CYCLES MODULO 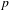 $p$ , II: SHIMURA CURVES
$p$ , II: SHIMURA CURVES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 07 May 2015, pp. 189-222
- Print publication:
- February 2017
-
- Article
- Export citation
THE JUMPING CHAMPION CONJECTURE
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 04 May 2015, pp. 719-740
- Print publication:
- September 2015
-
- Article
- Export citation

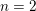
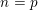
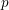
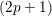
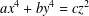
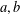

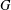
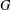
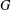
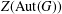
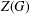
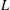
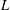
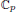 , the topological completion of the algebraic closure of the field of
, the topological completion of the algebraic closure of the field of 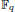 of q elements, we consider a trajectory of the map
of q elements, we consider a trajectory of the map 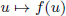 associated with a polynomial
associated with a polynomial 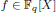 ]. Using bounds of character sums, under some mild condition on
]. Using bounds of character sums, under some mild condition on 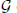 of
of 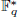 , improving the trivial lower bound
, improving the trivial lower bound 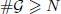 . Using a different technique, we also obtain a similar result for very small values of
. Using a different technique, we also obtain a similar result for very small values of  .
.