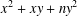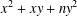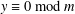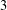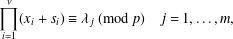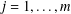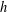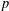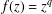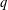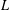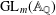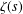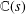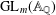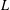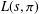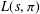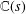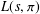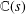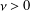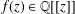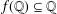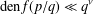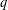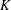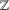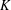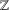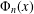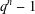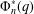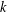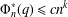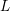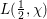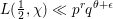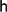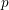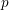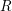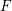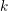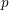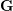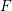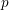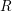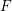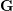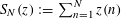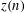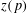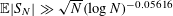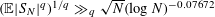Refine listing
Actions for selected content:
2818 results in 11xxx
REPRESENTATIONS OF INTEGERS BY THE BINARY QUADRATIC FORM
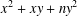 $x^{2}+xy+ny^{2}$
$x^{2}+xy+ny^{2}$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 17 November 2015, pp. 182-191
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
SYSTEMS OF CONGRUENCES WITH PRODUCTS OF VARIABLES FROM SHORT INTERVALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 11 November 2015, pp. 364-371
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
ON A PROBLEM POSED BY MAHLER
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 11 November 2015, pp. 86-107
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
HYPERTRANSCENDENCE OF
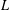 $L$-FUNCTIONS FOR
$L$-FUNCTIONS FOR 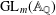 $\text{GL}_{m}(\mathbb{A}_{\mathbb{Q}})$
$\text{GL}_{m}(\mathbb{A}_{\mathbb{Q}})$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 11 November 2015, pp. 388-399
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
ON MULTIPLE ZETA VALUES OF EXTREMAL HEIGHT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 11 November 2015, pp. 186-193
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
CONGRUENCES MODULO 2 FOR CERTAIN PARTITION FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 11 November 2015, pp. 400-409
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
A NOTE ON LACUNARY POWER SERIES WITH RATIONAL COEFFICIENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 11 November 2015, pp. 372-374
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
ON THE MERTENS–CESÀRO THEOREM FOR NUMBER FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 11 November 2015, pp. 199-210
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
ON THE SQUARE-FREE REPRESENTATION FUNCTION OF A NORM FORM AND NILSEQUENCES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 11 November 2015, pp. 107-135
- Print publication:
- February 2018
-
- Article
- Export citation
PRIMITIVE PRIME DIVISORS AND THE
 $\mathbf{n}$ TH CYCLOTOMIC POLYNOMIAL
$\mathbf{n}$ TH CYCLOTOMIC POLYNOMIAL
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 04 November 2015, pp. 122-135
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
Sub-Weyl subconvexity for Dirichlet
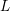 $L$-functions to prime power moduli
$L$-functions to prime power moduli
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 03 November 2015, pp. 825-875
- Print publication:
- April 2016
-
- Article
- Export citation
On n-Sums in an Abelian Group
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 3 / May 2016
- Published online by Cambridge University Press:
- 03 November 2015, pp. 419-435
-
- Article
- Export citation
Two compact incremental prime sieves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 November 2015, pp. 675-683
-
- Article
-
- You have access
- Export citation
CERTAIN GENERALIZED MORDELL CURVES OVER THE RATIONAL NUMBERS ARE POINTLESS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 28 October 2015, pp. 42-64
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
An explicit Baker-type lower bound of exponential values
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 6 / December 2015
- Published online by Cambridge University Press:
- 27 October 2015, pp. 1153-1182
- Print publication:
- December 2015
-
- Article
- Export citation
Ramanujan's Radial Limits and Mixed Mock Modular Bilateral q-Hypergeometric Series
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 26 October 2015, pp. 787-799
-
- Article
- Export citation
PERIODS OF AUTOMORPHIC FORMS: THE TRILINEAR CASE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 26 October 2015, pp. 59-74
- Print publication:
- February 2018
-
- Article
- Export citation
The pro-
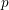 $p$-Iwahori Hecke algebra of a reductive
$p$-Iwahori Hecke algebra of a reductive 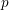 $p$-adic group I
$p$-adic group I
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 23 October 2015, pp. 693-753
- Print publication:
- April 2016
-
- Article
- Export citation
ADDITIVE DIMENSION AND A THEOREM OF SANDERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 22 October 2015, pp. 124-144
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
HELSON’S PROBLEM FOR SUMS OF A RANDOM MULTIPLICATIVE FUNCTION
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 21 October 2015, pp. 101-110
- Print publication:
- 2016
-
- Article
- Export citation