Refine listing
Actions for selected content:
2818 results in 11xxx
A DEFINABLE
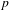 $p$ -ADIC ANALOGUE OF KIRSZBRAUN’S THEOREM ON EXTENSIONS OF LIPSCHITZ MAPS
$p$ -ADIC ANALOGUE OF KIRSZBRAUN’S THEOREM ON EXTENSIONS OF LIPSCHITZ MAPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 20 October 2015, pp. 39-57
- Print publication:
- February 2018
-
- Article
- Export citation
STARK POINTS AND
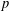 $p$-ADIC ITERATED INTEGRALS ATTACHED TO MODULAR FORMS OF WEIGHT ONE
$p$-ADIC ITERATED INTEGRALS ATTACHED TO MODULAR FORMS OF WEIGHT ONE
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 3 / 2015
- Published online by Cambridge University Press:
- 13 October 2015, e8
-
- Article
-
- You have access
- Open access
- Export citation
Simply connected varieties in characteristic
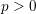 $p>0$
$p>0$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 2 / February 2016
- Published online by Cambridge University Press:
- 09 October 2015, pp. 255-287
- Print publication:
- February 2016
-
- Article
- Export citation
ON THE NUMBER OF DIVISORS OF
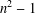 $n^{2}-1$
$n^{2}-1$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 02 October 2015, pp. 194-198
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
KUDLA’S MODULARITY CONJECTURE AND FORMAL FOURIER–JACOBI SERIES
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 3 / 2015
- Published online by Cambridge University Press:
- 01 October 2015, e7
-
- Article
-
- You have access
- Open access
- Export citation
CATEGORICITY OF MODULAR AND SHIMURA CURVES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 5 / November 2017
- Published online by Cambridge University Press:
- 30 September 2015, pp. 1075-1101
- Print publication:
- November 2017
-
- Article
- Export citation
ON THE LOCAL LANGLANDS CORRESPONDENCE FOR SPLIT CLASSICAL GROUPS OVER LOCAL FUNCTION FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 5 / November 2017
- Published online by Cambridge University Press:
- 30 September 2015, pp. 987-1074
- Print publication:
- November 2017
-
- Article
- Export citation
ELEMENTS OF ORDER FOUR IN THE NARROW CLASS GROUP OF REAL QUADRATIC FIELDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 28 September 2015, pp. 21-32
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
The Chowla–Selberg formula for abelian CM fields and Faltings heights
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 3 / March 2016
- Published online by Cambridge University Press:
- 24 September 2015, pp. 445-476
- Print publication:
- March 2016
-
- Article
- Export citation
EFFICIENT ALGORITHMS FOR TRAVELLING SALESMAN PROBLEMS ARISING IN WAREHOUSE ORDER PICKING
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 57 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 22 September 2015, pp. 166-174
-
- Article
-
- You have access
- Export citation
On the Number of Bh-Sets
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 16 September 2015, pp. 108-129
-
- Article
- Export citation
Sum of Many Dilates
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 3 / May 2016
- Published online by Cambridge University Press:
- 08 September 2015, pp. 460-469
-
- Article
- Export citation
Optimal cycles in ultrametric dynamics and minimally ramified power series
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 07 September 2015, pp. 187-222
- Print publication:
- January 2016
-
- Article
- Export citation
Arithmetic of positive characteristic
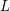 $L$-series values in Tate algebras
$L$-series values in Tate algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 07 September 2015, pp. 1-61
- Print publication:
- January 2016
-
- Article
- Export citation
Cusp forms on the exceptional group of type
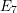 $E_{7}$
$E_{7}$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 2 / February 2016
- Published online by Cambridge University Press:
- 07 September 2015, pp. 223-254
- Print publication:
- February 2016
-
- Article
- Export citation
RESOLVABILITY PROPERTIES OF SIMILAR TOPOLOGIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 03 September 2015, pp. 470-477
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
Mordell’s equation: a classical approach
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 September 2015, pp. 633-646
-
- Article
-
- You have access
- Export citation
A quasi-linear time algorithm for computing modular polynomials in dimension 2
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 September 2015, pp. 603-632
-
- Article
-
- You have access
- Export citation
On spherical Monte Carlo simulations for multivariate normal probabilities
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 21 March 2016, pp. 817-836
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
p-adic Eisenstein-Kronecker series for CM elliptic curves and the Kronecker limit formulas
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 219 / September 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 269-302
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
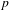
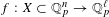
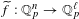
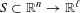
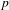
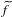
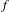
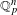
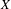
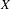
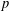
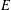
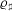
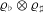
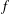
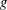
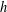
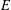
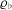
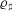
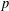
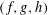
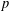
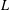
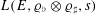
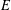
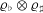
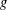
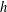
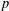
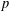
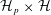
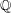
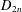
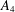
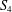
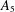
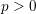
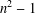
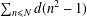
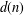

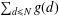
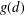

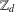
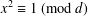
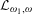
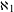
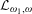
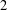
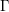
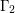
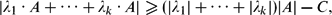
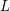
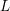
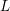
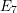
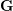
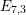
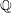
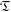
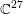
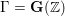
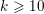
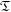
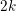
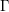
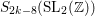
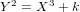

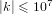

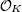 of K. In this paper, we construct
of K. In this paper, we construct 