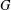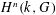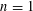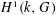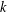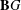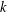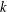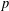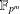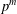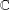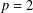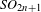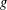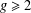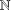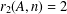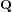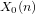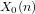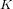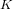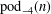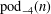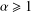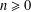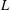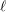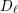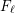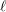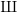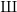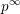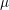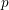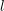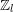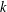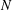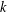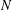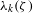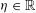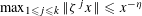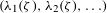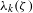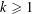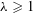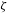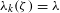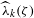Refine listing
Actions for selected content:
2818 results in 11xxx
TOPOLOGY ON COHOMOLOGY OF LOCAL FIELDS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 3 / 2015
- Published online by Cambridge University Press:
- 25 August 2015, e16
-
- Article
-
- You have access
- Open access
- Export citation
A REMARK ON TAIL DISTRIBUTIONS OF PARTITION RANK AND CRANK
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 20 August 2015, pp. 31-36
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
PARAMETRIZING ELLIPTIC CURVES BY MODULAR UNITS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 19 August 2015, pp. 33-41
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
MORE CONSTRUCTIONS OF APPROXIMATELY MUTUALLY UNBIASED BASES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 17 August 2015, pp. 211-222
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
NON-ARCHIMEDEAN YOMDIN–GROMOV PARAMETRIZATIONS AND POINTS OF BOUNDED HEIGHT
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 3 / 2015
- Published online by Cambridge University Press:
- 14 August 2015, e5
-
- Article
-
- You have access
- Open access
- Export citation
THE DOUBLE COVER OF ODD GENERAL SPIN GROUPS, SMALL REPRESENTATIONS, AND APPLICATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 07 August 2015, pp. 609-671
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
Formal Fourier Jacobi expansions and special cycles of codimension two
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 12 / December 2015
- Published online by Cambridge University Press:
- 06 August 2015, pp. 2187-2211
- Print publication:
- December 2015
-
- Article
- Export citation
ON MINIMAL ASYMPTOTIC
 $g$-ADIC BASES
$g$-ADIC BASES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 05 August 2015, pp. 374-379
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
Examples of CM curves of genus two defined over the reflex field
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 August 2015, pp. 507-538
-
- Article
-
- You have access
- Export citation
Hyperelliptic modular curves
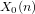 $X_{0}(n)$ and isogenies of elliptic curves over quadratic fields
$X_{0}(n)$ and isogenies of elliptic curves over quadratic fields
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 August 2015, pp. 578-602
-
- Article
-
- You have access
- Export citation
FACTORIALS AND THE RAMANUJAN FUNCTION
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 177-185
- Print publication:
- January 2016
-
- Article
-
- You have access
- Export citation
ON THE NUMBER OF RATIONAL POINTS ON PRYM VARIETIES OVER FINITE FIELDS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 55-68
- Print publication:
- January 2016
-
- Article
-
- You have access
- Export citation
EXCEPTIONAL ZEROES OF P-ADIC L-FUNCTIONS OVER NON-ABELIAN FIELD EXTENSIONS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 385-432
- Print publication:
- May 2016
-
- Article
-
- You have access
- Export citation
ARITHMETIC PROPERTIES OF PARTITION QUADRUPLES WITH ODD PARTS DISTINCT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 08 July 2015, pp. 353-364
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
A NOTE ON SIMPLE ZEROS OF PRIMITIVE DIRICHLET
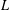 $L$-FUNCTIONS
$L$-FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 08 July 2015, pp. 19-30
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
An Improvement of the Beck–Fiala Theorem
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 3 / May 2016
- Published online by Cambridge University Press:
- 06 July 2015, pp. 380-398
-
- Article
- Export citation
Identities for field extensions generalizing the Ohno–Nakagawa relations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 11 / November 2015
- Published online by Cambridge University Press:
- 30 June 2015, pp. 2059-2075
- Print publication:
- November 2015
-
- Article
- Export citation
Growth of
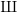 $\unicode[STIX]{x0428}$ in towers for isogenous curves
$\unicode[STIX]{x0428}$ in towers for isogenous curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 11 / November 2015
- Published online by Cambridge University Press:
- 30 June 2015, pp. 1981-2005
- Print publication:
- November 2015
-
- Article
- Export citation
AVERAGES OF TWISTED
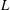 $L$-FUNCTIONS
$L$-FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 24 June 2015, pp. 207-236
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
ON THE SPECTRUM OF DIOPHANTINE APPROXIMATION CONSTANTS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 22 June 2015, pp. 79-100
- Print publication:
- 2016
-
- Article
- Export citation