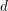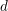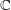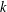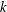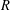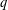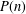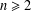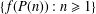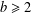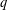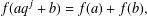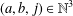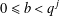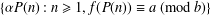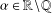Refine listing
Actions for selected content:
2818 results in 11xxx
PRIMES IN BEATTY SEQUENCES IN SHORT INTERVALS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 17 February 2016, pp. 572-586
- Print publication:
- 2016
-
- Article
- Export citation
OPPOSITE-SIGN KLOOSTERMAN SUM ZETA FUNCTION
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 28 January 2016, pp. 406-429
- Print publication:
- 2016
-
- Article
- Export citation
A GENERALIZATION OF THE DISCRETE VERSION OF MINKOWSKI’S FUNDAMENTAL THEOREM
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 29 February 2016, pp. 637-652
- Print publication:
- 2016
-
- Article
- Export citation
ON THE THETA OPERATOR FOR MODULAR FORMS MODULO PRIME POWERS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 22 January 2016, pp. 321-336
- Print publication:
- 2016
-
- Article
- Export citation
EXPONENTIAL SUMS OVER PRIMES IN SHORT INTERVALS AND AN APPLICATION TO THE WARING–GOLDBACH PROBLEM
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 17 February 2016, pp. 508-523
- Print publication:
- 2016
-
- Article
- Export citation
A DICHOTOMY LAW FOR THE DIOPHANTINE PROPERTIES IN
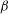 $\unicode[STIX]{x1D6FD}$ -DYNAMICAL SYSTEMS
$\unicode[STIX]{x1D6FD}$ -DYNAMICAL SYSTEMS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 16 May 2016, pp. 884-897
- Print publication:
- 2016
-
- Article
- Export citation
THE PROPORTION OF FAILURES OF THE HASSE NORM PRINCIPLE
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 22 January 2016, pp. 337-347
- Print publication:
- 2016
-
- Article
- Export citation
ON SMALL BASES FOR WHICH 1 HAS COUNTABLY MANY EXPANSIONS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 22 January 2016, pp. 362-377
- Print publication:
- 2016
-
- Article
- Export citation
On the sum of the square of a prime and a square-free number
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 January 2016, pp. 16-24
-
- Article
-
- You have access
- Export citation
SIGN OF FOURIER COEFFICIENTS OF MODULAR FORMS OF HALF-INTEGRAL WEIGHT
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 17 May 2016, pp. 866-883
- Print publication:
- 2016
-
- Article
- Export citation
Rational Values of Weierstrass Zeta Functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 22 December 2015, pp. 945-958
-
- Article
- Export citation
Strict supports of canonical measures and applications to the geometric Bogomolov conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 22 December 2015, pp. 997-1040
- Print publication:
- May 2016
-
- Article
- Export citation
Arithmetic Density
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 14 December 2015, pp. 691-700
-
- Article
- Export citation
Integral canonical models for Spin Shimura varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 07 December 2015, pp. 769-824
- Print publication:
- April 2016
-
- Article
- Export citation
On
 ${\it\lambda}$ -invariants attached to cyclic cubic number fields
${\it\lambda}$ -invariants attached to cyclic cubic number fields
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 December 2015, pp. 684-698
-
- Article
-
- You have access
- Export citation
Good families of Drinfeld modular curves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 December 2015, pp. 699-712
-
- Article
-
- You have access
- Export citation
On a generalization of a waiting time problem and some combinatorial identities
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 30 March 2016, pp. 981-989
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
Integral points of bounded degree on affine curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 26 November 2015, pp. 754-768
- Print publication:
- April 2016
-
- Article
- Export citation
FACTORS OF CARMICHAEL NUMBERS AND A WEAK
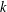 $k$-TUPLES CONJECTURE
$k$-TUPLES CONJECTURE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 17 November 2015, pp. 421-429
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
STRONGLY
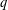 $q$-ADDITIVE FUNCTIONS AND DISTRIBUTIONAL PROPERTIES OF THE LARGEST PRIME FACTOR
$q$-ADDITIVE FUNCTIONS AND DISTRIBUTIONAL PROPERTIES OF THE LARGEST PRIME FACTOR
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 17 November 2015, pp. 177-185
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
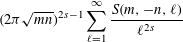
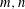
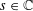
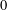
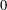
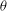
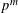
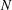
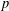
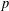
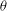
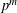
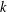
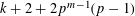
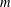
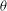
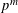
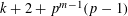
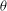
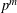
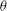
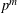
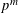
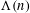

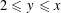
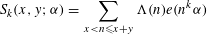



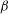
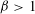
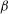
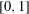
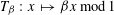
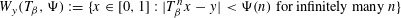
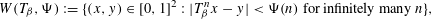
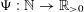

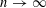
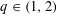
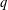

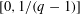
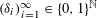
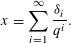
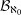
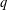

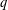
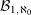
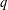
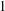
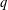
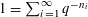
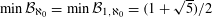
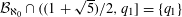
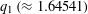
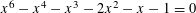
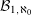
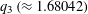
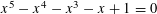
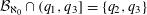
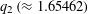
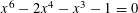
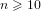
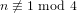
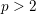
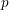
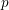

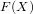

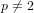
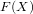

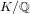
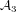
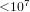
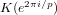
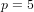
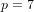



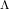
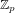
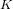
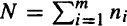 Let
Let