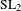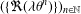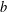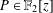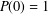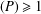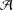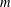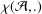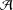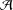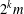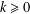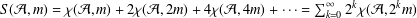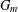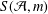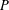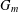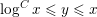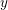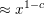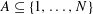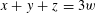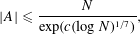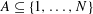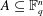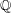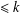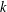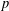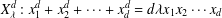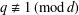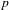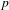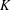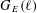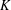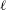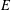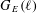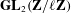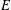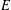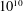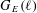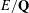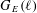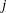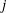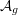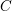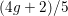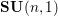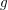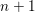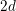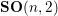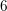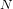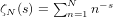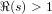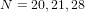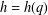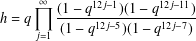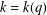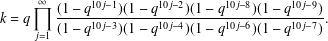Refine listing
Actions for selected content:
2818 results in 11xxx
Numerical semigroups with a given set of pseudo-Frobenius numbers
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 April 2016, pp. 186-205
-
- Article
-
- You have access
- Export citation
 $L$ -INDISTINGUISHABILITY ON EIGENVARIETIES
$L$ -INDISTINGUISHABILITY ON EIGENVARIETIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 22 March 2016, pp. 425-440
- Print publication:
- April 2018
-
- Article
- Export citation
Some applications of eta-quotients
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 22 March 2016, pp. 565-578
- Print publication:
- June 2016
-
- Article
- Export citation
ON REAL PARTS OF POWERS OF COMPLEX PISOT NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 245-253
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
ABSOLUTELY ABNORMAL AND CONTINUED FRACTION NORMAL NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 217-223
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
SETS WITH EVEN PARTITION FUNCTIONS AND CYCLOTOMIC NUMBERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 14 March 2016, pp. 289-302
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
WILDER MCKAY CORRESPONDENCES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 221 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 15 March 2016, pp. 111-164
- Print publication:
- March 2016
-
- Article
-
- You have access
- HTML
- Export citation
Minor arcs, mean values, and restriction theory for exponential sums over smooth numbers
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 6 / June 2016
- Published online by Cambridge University Press:
- 23 February 2016, pp. 1121-1158
- Print publication:
- June 2016
-
- Article
- Export citation
ROTH’S THEOREM FOR FOUR VARIABLES AND ADDITIVE STRUCTURES IN SUMS OF SPARSE SETS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 19 February 2016, e5
-
- Article
-
- You have access
- Open access
- Export citation
GENERALIZED EXPLICIT DESCENT AND ITS APPLICATION TO CURVES OF GENUS 3
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 17 February 2016, e6
-
- Article
-
- You have access
- Open access
- Export citation
ALGORITHMS FOR GALOIS EXTENSIONS OF GLOBAL FUNCTION FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 17 February 2016, pp. 513-515
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
REFINEMENTS OF THE FIRST AND SECOND POSITIVE CRANK MOMENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 17 February 2016, pp. 236-244
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
COUNTING POINTS ON DWORK HYPERSURFACES AND
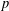 $p$ -ADIC HYPERGEOMETRIC FUNCTIONS
$p$ -ADIC HYPERGEOMETRIC FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 17 February 2016, pp. 208-216
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
ON THE EXCEPTIONAL SPECIALIZATIONS OF BIG HEEGNER POINTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 04 February 2016, pp. 207-240
- Print publication:
- February 2018
-
- Article
- Export citation
COMPUTING IMAGES OF GALOIS REPRESENTATIONS ATTACHED TO ELLIPTIC CURVES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 02 February 2016, e4
-
- Article
-
- You have access
- Open access
- Export citation
On the Oort conjecture for Shimura varieties of unitary and orthogonal types
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 02 February 2016, pp. 889-917
- Print publication:
- May 2016
-
- Article
- Export citation
Real-dihedral harmonic Maass forms and CM-values of Hilbert modular functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 6 / June 2016
- Published online by Cambridge University Press:
- 02 February 2016, pp. 1159-1197
- Print publication:
- June 2016
-
- Article
- Export citation
Zeroes of partial sums of the zeta-function
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 February 2016, pp. 37-41
-
- Article
-
- You have access
- Export citation
THE LEVEL 12 ANALOGUE OF RAMANUJAN’S FUNCTION
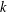 $k$
$k$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 22 January 2016, pp. 29-53
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
Relative Manin–Mumford for Semi-Abelian Surfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 18 January 2016, pp. 837-875
-
- Article
- Export citation