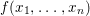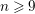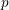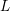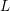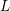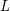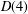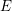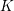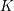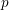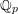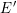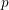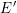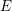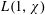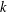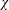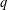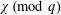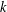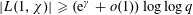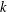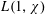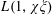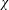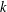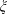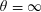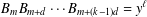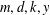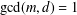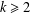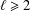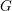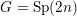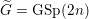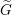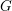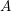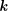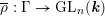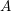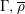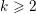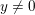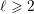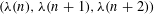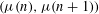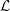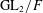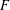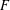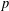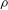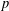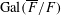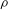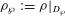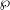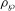Refine listing
Actions for selected content:
2818 results in 11xxx
THE QUADRATIC FORM IN NINE PRIME VARIABLES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 223 / Issue 1 / September 2016
- Published online by Cambridge University Press:
- 18 August 2016, pp. 21-65
- Print publication:
- September 2016
-
- Article
-
- You have access
- HTML
- Export citation
PAIR CORRELATION OF LOW-LYING ZEROS OF QUADRATIC
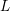 $L$ -FUNCTIONS
$L$ -FUNCTIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 223 / Issue 1 / September 2016
- Published online by Cambridge University Press:
- 18 August 2016, pp. 87-135
- Print publication:
- September 2016
-
- Article
-
- You have access
- HTML
- Export citation
AN UPPER BOUND FOR THE NUMBER OF DIOPHANTINE QUINTUPLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 16 August 2016, pp. 384-394
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
IMAGES OF ADELIC GALOIS REPRESENTATIONS FOR MODULAR FORMS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 03 August 2016, pp. 11-25
- Print publication:
- January 2017
-
- Article
-
- You have access
- Export citation
The remaining cases of the Kramer–Tunnell conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 11 / November 2016
- Published online by Cambridge University Press:
- 29 July 2016, pp. 2255-2268
- Print publication:
- November 2016
-
- Article
- Export citation
RESTRICTED SIMULTANEOUS DIOPHANTINE APPROXIMATION
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 26 July 2016, pp. 34-52
- Print publication:
- 2017
-
- Article
- Export citation
LARGE VALUES OF
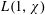 $L(1,\unicode[STIX]{x1D712})$ FOR
$L(1,\unicode[STIX]{x1D712})$ FOR 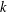 $k$ TH ORDER CHARACTERS
$k$ TH ORDER CHARACTERS 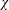 $\unicode[STIX]{x1D712}$ AND APPLICATIONS TO CHARACTER SUMS
$\unicode[STIX]{x1D712}$ AND APPLICATIONS TO CHARACTER SUMS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 26 July 2016, pp. 53-71
- Print publication:
- 2017
-
- Article
- Export citation
THE
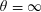 $\unicode[STIX]{x1D703}=\infty$ CONJECTURE IMPLIES THE RIEMANN HYPOTHESIS
$\unicode[STIX]{x1D703}=\infty$ CONJECTURE IMPLIES THE RIEMANN HYPOTHESIS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 26 July 2016, pp. 29-33
- Print publication:
- 2017
-
- Article
- Export citation
PERFECT POWERS IN PRODUCTS OF TERMS OF ELLIPTIC DIVISIBILITY SEQUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 21 July 2016, pp. 395-404
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
TORSION GALOIS REPRESENTATIONS OVER CM FIELDS AND HECKE ALGEBRAS IN THE DERIVED CATEGORY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 21 July 2016, e21
-
- Article
-
- You have access
- Open access
- Export citation
ANDRÉ–OORT CONJECTURE AND NONVANISHING OF CENTRAL
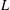 $L$ -VALUES OVER HILBERT CLASS FIELDS
$L$ -VALUES OVER HILBERT CLASS FIELDS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 20 July 2016, e20
-
- Article
-
- You have access
- Open access
- Export citation
The genus, Frobenius number and pseudo-Frobenius numbers of numerical semigroups of type 2
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 5 / October 2016
- Published online by Cambridge University Press:
- 19 July 2016, pp. 1081-1090
- Print publication:
- October 2016
-
- Article
- Export citation
On a lifting problem of L-packets
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 9 / September 2016
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1800-1850
- Print publication:
- September 2016
-
- Article
- Export citation
The inverse deformation problem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 8 / August 2016
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1725-1739
- Print publication:
- August 2016
-
- Article
- Export citation
Rational points on Erdős–Selfridge superelliptic curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 11 / November 2016
- Published online by Cambridge University Press:
- 14 July 2016, pp. 2249-2254
- Print publication:
- November 2016
-
- Article
- Export citation
Sur les processus arithmétiques liés aux diviseurs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue A / July 2016
- Published online by Cambridge University Press:
- 25 July 2016, pp. 63-76
- Print publication:
- July 2016
-
- Article
- Export citation
SIGN PATTERNS OF THE LIOUVILLE AND MÖBIUS FUNCTIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 21 June 2016, e14
-
- Article
-
- You have access
- Open access
- Export citation
A NOTE ON WEIGHTED BADLY APPROXIMABLE LINEAR FORMS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 349-357
- Print publication:
- May 2017
-
- Article
-
- You have access
- Export citation
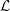 ${\mathcal{L}}$ -INVARIANTS AND LOCAL–GLOBAL COMPATIBILITY FOR THE GROUP
${\mathcal{L}}$ -INVARIANTS AND LOCAL–GLOBAL COMPATIBILITY FOR THE GROUP 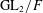 $\text{GL}_{2}/F$
$\text{GL}_{2}/F$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 10 June 2016, e13
-
- Article
-
- You have access
- Open access
- Export citation
A TRACE FORMULA FOR HECKE OPERATORS ON VECTOR-VALUED MODULAR FORMS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 143-165
- Print publication:
- January 2017
-
- Article
-
- You have access
- Export citation