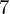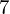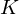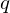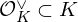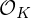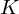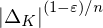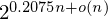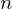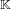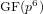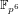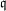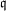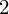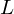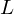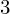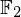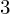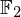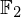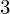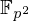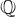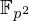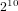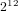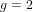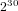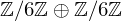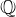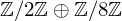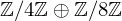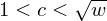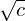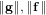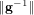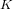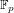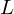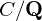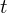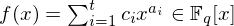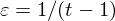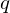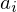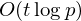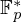Refine listing
Actions for selected content:
2818 results in 11xxx
Visualizing elements of order
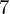 $7$ in the Tate–Shafarevich group of an elliptic curve
$7$ in the Tate–Shafarevich group of an elliptic curve
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 100-114
-
- Article
-
- You have access
- Export citation
On error distributions in ring-based LWE
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 130-145
-
- Article
-
- You have access
- Export citation
Tuple lattice sieving
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 146-162
-
- Article
-
- You have access
- Export citation
Point counting on K3 surfaces and an application concerning real and complex multiplication
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 12-28
-
- Article
-
- You have access
- Export citation
Computing Jacobi forms
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 205-219
-
- Article
-
- You have access
- Export citation
Computing canonical heights on elliptic curves in quasi-linear time
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 391-405
-
- Article
-
- You have access
- Export citation
Reducing number field defining polynomials: an application to class group computations
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 315-331
-
- Article
-
- You have access
- Export citation
Fast heuristic algorithms for computing relations in the class group of a quadratic order, with applications to isogeny evaluation
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 371-390
-
- Article
-
- You have access
- Export citation
Collecting relations for the number field sieve in
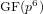 $\text{GF}(p^{6})$
$\text{GF}(p^{6})$
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 332-350
-
- Article
-
- You have access
- Export citation
A database of genus-2 curves over the rational numbers
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 235-254
-
- Article
-
- You have access
- Export citation
A census of zeta functions of quartic K
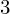 $3$ surfaces over
$3$ surfaces over 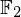 $\mathbb{F}_{2}$
$\mathbb{F}_{2}$
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 1-11
-
- Article
-
- You have access
- Export citation
Computing cardinalities of
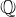 $\mathbb{Q}$ -curve reductions over finite fields
$\mathbb{Q}$ -curve reductions over finite fields
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 115-129
-
- Article
-
- You have access
- Export citation
Character theory approach to Sato–Tate groups
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 301-314
-
- Article
-
- You have access
- Export citation
JKL-ECM: an implementation of ECM using Hessian curves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 83-99
-
- Article
-
- You have access
- Export citation
Reduced memory meet-in-the-middle attackagainst the NTRU private key
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 43-57
-
- Article
-
- You have access
- Export citation
Algorithms for the approximate common divisor problem
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 58-72
-
- Article
-
- You have access
- Export citation
An algorithm for NTRU problems and cryptanalysis of the GGH multilinear map without a low-level encoding of zero
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 255-266
-
- Article
-
- You have access
- Export citation
Constructing genus-3 hyperelliptic Jacobians with CM
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 283-300
-
- Article
-
- You have access
- Export citation
Computing
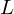 $L$ -series of geometrically hyperelliptic curvesof genus three
$L$ -series of geometrically hyperelliptic curvesof genus three
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 220-234
-
- Article
-
- You have access
- Export citation
Roots of sparse polynomials over a finite field
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 196-204
-
- Article
-
- You have access
- Export citation