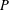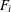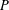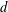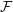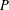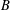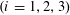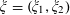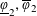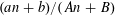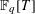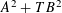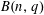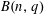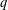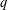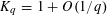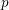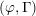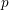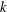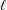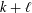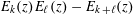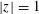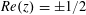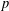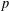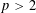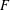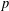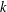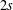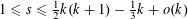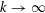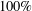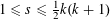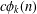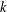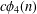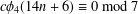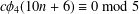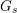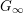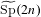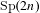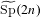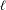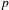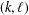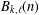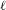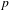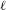Refine listing
Actions for selected content:
2816 results in 11xxx
ON MULTIPLICATIVE COMPOSITIONS OF INTEGERS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 1081-1090
- Print publication:
- 2017
-
- Article
- Export citation
PRIME NUMBER THEOREM EQUIVALENCES AND NON-EQUIVALENCES
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 852-862
- Print publication:
- 2017
-
- Article
- Export citation
TIGHTER BOUNDS FOR THE DISCREPANCY OF BOXESAND POLYTOPES
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 1091-1113
- Print publication:
- 2017
-
- Article
- Export citation
DISCREPANCY OF SECOND ORDER DIGITAL SEQUENCES IN FUNCTION SPACES WITH DOMINATING MIXED SMOOTHNESS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 863-894
- Print publication:
- 2017
-
- Article
- Export citation
SIMULTANEOUS APPROXIMATION TO TWO REALS: BOUNDS FOR THE SECOND SUCCESSIVE MINIMUM
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 1136-1151
- Print publication:
- 2017
-
- Article
- Export citation
HARMONIC ANALYSIS ON THE POSITIVE RATIONALS. DETERMINATION OF THE GROUP GENERATED BY THE RATIOS
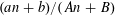 $(an+b)/(An+B)$
$(an+b)/(An+B)$
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 919-943
- Print publication:
- 2017
-
- Article
- Export citation
A POLYNOMIAL ANALOGUE OF LANDAU’S THEOREM AND RELATED PROBLEMS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 05 June 2017, pp. 622-665
- Print publication:
- 2017
-
- Article
- Export citation
Paraboline variation over
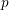 $p$ -adic families of
$p$ -adic families of 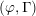 $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$ -modules
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$ -modules
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 19 January 2017, pp. 132-174
- Print publication:
- January 2017
-
- Article
- Export citation
ZEROS OF CERTAIN COMBINATIONS OF EISENSTEIN SERIES
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 10 August 2017, pp. 666-695
- Print publication:
- 2017
-
- Article
- Export citation
SERRE WEIGHTS AND WILD RAMIFICATION IN TWO-DIMENSIONAL GALOIS REPRESENTATIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 23 December 2016, e33
-
- Article
-
- You have access
- Open access
- Export citation
APPROXIMATING THE MAIN CONJECTURE IN VINOGRADOV’S MEAN VALUE THEOREM
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 21 December 2016, pp. 292-350
- Print publication:
- 2017
-
- Article
- Export citation
CONGRUENCES MODULO 5 AND 7 FOR 4-COLORED GENERALIZED FROBENIUS PARTITIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 21 December 2016, pp. 157-176
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
ON GALOIS EQUIVARIANCE OF HOMOMORPHISMS BETWEEN TORSION CRYSTALLINE REPRESENTATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 229 / March 2018
- Published online by Cambridge University Press:
- 13 December 2016, pp. 169-214
- Print publication:
- March 2018
-
- Article
-
- You have access
- HTML
- Export citation
SPECTRAL TRANSFER FOR METAPLECTIC GROUPS. I. LOCAL CHARACTER RELATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 07 December 2016, pp. 25-123
- Print publication:
- January 2019
-
- Article
- Export citation
ON THE COHOMOLOGY OF SOME SIMPLE SHIMURA VARIETIES WITH BAD REDUCTION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 06 December 2016, pp. 1-24
- Print publication:
- January 2019
-
- Article
- Export citation
ARITHMETIC PROPERTIES OF
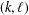 $(k,\ell )$ -REGULAR BIPARTITIONS
$(k,\ell )$ -REGULAR BIPARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 01 December 2016, pp. 353-364
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
ON THE EXPANSIONS OF REAL NUMBERS IN TWO MULTIPLICATIVELY DEPENDENT BASES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 01 December 2016, pp. 373-383
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
ON THE
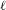 $\ell$-ADIC COHOMOLOGY OF SOME
$\ell$-ADIC COHOMOLOGY OF SOME 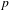 $p$-ADICALLY UNIFORMIZED SHIMURA VARIETIES
$p$-ADICALLY UNIFORMIZED SHIMURA VARIETIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 5 / November 2018
- Published online by Cambridge University Press:
- 01 December 2016, pp. 1197-1226
- Print publication:
- November 2018
-
- Article
- Export citation
SPECTRAL ZETA FUNCTIONS FOR THE QUANTUM RABI MODELS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 229 / March 2018
- Published online by Cambridge University Press:
- 01 December 2016, pp. 52-98
- Print publication:
- March 2018
-
- Article
-
- You have access
- HTML
- Export citation
WEIGHT CHANGING OPERATORS FOR AUTOMORPHIC FORMS ON GRASSMANNIANS AND DIFFERENTIAL PROPERTIES OF CERTAIN THETA LIFTS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 228 / December 2017
- Published online by Cambridge University Press:
- 28 November 2016, pp. 186-221
- Print publication:
- December 2017
-
- Article
-
- You have access
- HTML
- Export citation