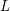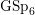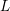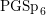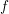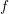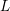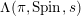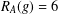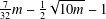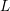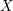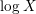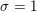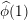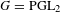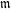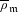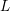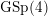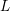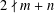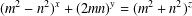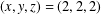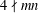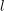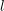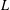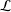Refine listing
Actions for selected content:
2816 results in 11xxx
On descending cohomology geometrically
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 7 / July 2017
- Published online by Cambridge University Press:
- 10 May 2017, pp. 1446-1478
- Print publication:
- July 2017
-
- Article
- Export citation
The spin
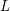 $L$ -function on
$L$ -function on 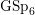 $\text{GSp}_{6}$ for Siegel modular forms
$\text{GSp}_{6}$ for Siegel modular forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 7 / July 2017
- Published online by Cambridge University Press:
- 10 May 2017, pp. 1391-1432
- Print publication:
- July 2017
-
- Article
- Export citation
MULTI-POLY-BERNOULLI NUMBERS AND RELATED ZETA FUNCTIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 232 / December 2018
- Published online by Cambridge University Press:
- 08 May 2017, pp. 19-54
- Print publication:
- December 2018
-
- Article
-
- You have access
- HTML
- Export citation
THE DOUBLE SHUFFLE RELATIONS FOR MULTIPLE EISENSTEIN SERIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 230 / June 2018
- Published online by Cambridge University Press:
- 08 May 2017, pp. 180-212
- Print publication:
- June 2018
-
- Article
-
- You have access
- HTML
- Export citation
ON ADDITIVE REPRESENTATION FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 02 May 2017, pp. 380-388
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
On the topology of Diophantine approximation spectra
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 7 / July 2017
- Published online by Cambridge University Press:
- 02 May 2017, pp. 1512-1546
- Print publication:
- July 2017
-
- Article
- Export citation
On the fourth moment of Hecke–Maass forms and the random wave conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 7 / July 2017
- Published online by Cambridge University Press:
- 02 May 2017, pp. 1479-1511
- Print publication:
- July 2017
-
- Article
- Export citation
Low-lying zeros of quadratic Dirichlet
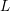 $L$ -functions: lower order terms for extended support
$L$ -functions: lower order terms for extended support
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 6 / June 2017
- Published online by Cambridge University Press:
- 26 April 2017, pp. 1196-1216
- Print publication:
- June 2017
-
- Article
- Export citation
BEYOND ENDOSCOPY FOR THE RELATIVE TRACE FORMULA II: GLOBAL THEORY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 2 / March 2019
- Published online by Cambridge University Press:
- 24 April 2017, pp. 347-447
- Print publication:
- March 2019
-
- Article
- Export citation
Vinogradov’s three primes theorem with almost twin primes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 6 / June 2017
- Published online by Cambridge University Press:
- 20 April 2017, pp. 1220-1256
- Print publication:
- June 2017
-
- Article
- Export citation
RATIONAL POINTS ON SHIMURA CURVES AND THE MANIN OBSTRUCTION
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 230 / June 2018
- Published online by Cambridge University Press:
- 12 April 2017, pp. 144-159
- Print publication:
- June 2018
-
- Article
-
- You have access
- HTML
- Export citation
Rapoport–Zink spaces for spinor groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 5 / May 2017
- Published online by Cambridge University Press:
- 10 April 2017, pp. 1050-1118
- Print publication:
- May 2017
-
- Article
- Export citation
PROPRIÉTÉS LOCALES DES CHIFFRES DES NOMBRES PREMIERS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 04 April 2017, pp. 189-224
- Print publication:
- January 2019
-
- Article
- Export citation
SUR LA TORSION DANS LA COHOMOLOGIE DES VARIÉTÉS DE SHIMURA DE KOTTWITZ-HARRIS-TAYLOR
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 3 / May 2019
- Published online by Cambridge University Press:
- 30 March 2017, pp. 499-517
- Print publication:
- May 2019
-
- Article
- Export citation
On higher regulators of Siegel threefolds II: the connection to the special value
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 5 / May 2017
- Published online by Cambridge University Press:
- 27 March 2017, pp. 889-946
- Print publication:
- May 2017
-
- Article
- Export citation
Construction of ray-class fields by smaller generators and their applications
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 20 March 2017, pp. 781-812
- Print publication:
- August 2017
-
- Article
- Export citation
Congruences concerning truncated hypergeometric series
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 16 March 2017, pp. 599-613
- Print publication:
- June 2017
-
- Article
- Export citation
JEŚMANOWICZ’ CONJECTURE ON PYTHAGOREAN TRIPLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 30-35
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
Bezout-type theorems for differential fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 4 / April 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 867-888
- Print publication:
- April 2017
-
- Article
- Export citation
ON ALGEBRAIC DIFFERENTIAL EQUATIONS FOR THE GAMMA FUNCTION AND
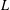 $L$ -FUNCTIONS IN THE EXTENDED SELBERG CLASS
$L$ -FUNCTIONS IN THE EXTENDED SELBERG CLASS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 36-43
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation