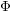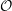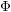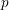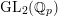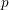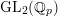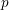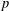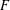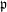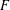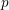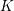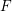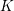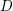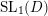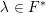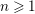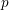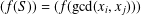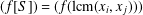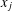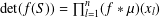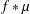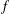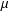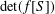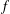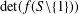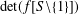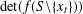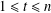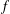Refine listing
Actions for selected content:
2816 results in 11xxx
LIPSCHITZ EQUIVALENCE OF CANTOR SETS AND IRREDUCIBILITY OF POLYNOMIALS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 3 / 2018
- Published online by Cambridge University Press:
- 26 June 2018, pp. 730-741
- Print publication:
- 2018
-
- Article
- Export citation
THE DENSITY OF NUMBERS REPRESENTED BY DIAGONAL FORMS OF LARGE DEGREE
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 23 April 2018, pp. 542-550
- Print publication:
- 2018
-
- Article
- Export citation
Corrigendum: Torsion points on abelian varieties of CM-type
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 3 / March 2018
- Published online by Cambridge University Press:
- 26 December 2017, p. 594
- Print publication:
- March 2018
-
- Article
-
- You have access
- HTML
- Export citation
Cluster algebras and continued fractions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 3 / March 2018
- Published online by Cambridge University Press:
- 22 December 2017, pp. 565-593
- Print publication:
- March 2018
-
- Article
- Export citation
GROUP ACTION ON THE DEFORMATIONS OF A FORMAL GROUP OVER THE RING OF WITT VECTORS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 235 / September 2019
- Published online by Cambridge University Press:
- 20 December 2017, pp. 42-57
- Print publication:
- September 2019
-
- Article
-
- You have access
- HTML
- Export citation
A note on multiplicative functions on progressions to large moduli
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 04 December 2017, pp. 63-77
- Print publication:
- February 2018
-
- Article
- Export citation
Patching and the
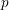 $p$ -adic Langlands program for
$p$ -adic Langlands program for 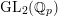 $\operatorname{GL}_{2}(\mathbb{Q}_{p})$
$\operatorname{GL}_{2}(\mathbb{Q}_{p})$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 3 / March 2018
- Published online by Cambridge University Press:
- 01 December 2017, pp. 503-548
- Print publication:
- March 2018
-
- Article
- Export citation
UNRAMIFIEDNESS OF GALOIS REPRESENTATIONS ARISING FROM HILBERT MODULAR SURFACES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 23 November 2017, e29
-
- Article
-
- You have access
- Open access
- Export citation
GENERALISED DIVISOR SUMS OF BINARY FORMS OVER NUMBER FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 16 November 2017, pp. 137-173
- Print publication:
- January 2020
-
- Article
- Export citation
AX–SCHANUEL CONDITION IN ARBITRARY CHARACTERISTIC
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 6 / November 2019
- Published online by Cambridge University Press:
- 08 November 2017, pp. 1157-1213
- Print publication:
- November 2019
-
- Article
- Export citation
Local–global principle for reduced norms over function fields of
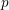 $p$ -adic curves
$p$ -adic curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 2 / February 2018
- Published online by Cambridge University Press:
- 02 November 2017, pp. 410-458
- Print publication:
- February 2018
-
- Article
- Export citation
TWO-DIMENSIONAL SHRINKING TARGET PROBLEM IN BETA-DYNAMICAL SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 02 November 2017, pp. 33-42
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
ON THE RESIDUE OF EISENSTEIN CLASSES OF SIEGEL VARIETIES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 30 October 2017, pp. 539-553
- Print publication:
- September 2018
-
- Article
-
- You have access
- Export citation
A MODULI INTERPRETATION FOR THE NON-SPLIT CARTAN MODULAR CURVE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 30 October 2017, pp. 411-434
- Print publication:
- May 2018
-
- Article
-
- You have access
- Export citation
Odd zeta motive and linear forms in odd zeta values
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 2 / February 2018
- Published online by Cambridge University Press:
- 30 October 2017, pp. 342-379
- Print publication:
- February 2018
-
- Article
- Export citation
LOCAL BORCHERDS PRODUCTS FOR UNITARY GROUPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 234 / June 2019
- Published online by Cambridge University Press:
- 27 October 2017, pp. 139-169
- Print publication:
- June 2019
-
- Article
-
- You have access
- HTML
- Export citation
INTERPOLATED SCHUR MULTIPLE ZETA VALUES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 25 October 2017, pp. 289-307
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
MULTIPLICATIVE ORDERS IN ORBITS OF POLYNOMIALS OVER FINITE FIELDS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 23 October 2017, pp. 487-493
- Print publication:
- May 2018
-
- Article
-
- You have access
- Export citation
Arithmetic properties of Apéry-like numbers
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 2 / February 2018
- Published online by Cambridge University Press:
- 20 October 2017, pp. 249-274
- Print publication:
- February 2018
-
- Article
- Export citation
MORE ON A CERTAIN ARITHMETICAL DETERMINANT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 17 October 2017, pp. 15-25
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation