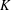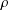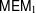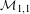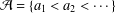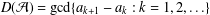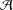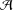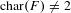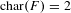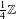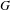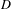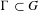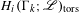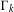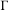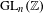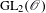Refine listing
Actions for selected content:
2816 results in 11xxx
Arithmetic intersection on GSpin Rapoport–Zink spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 7 / July 2018
- Published online by Cambridge University Press:
- 16 May 2018, pp. 1407-1440
- Print publication:
- July 2018
-
- Article
- Export citation
Duality for relative logarithmic de Rham–Witt sheaves and wildly ramified class field theory over finite fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 6 / June 2018
- Published online by Cambridge University Press:
- 07 May 2018, pp. 1306-1331
- Print publication:
- June 2018
-
- Article
- Export citation
BOUNDS FOR TRIPLE EXPONENTIAL SUMS WITH MIXED EXPONENTIAL AND LINEAR TERMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 03 May 2018, pp. 64-69
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
COMMON SLOTS OF BILINEAR AND QUADRATIC PFISTER FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 03 May 2018, pp. 38-47
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
MAHLER MEASURE OF ‘ALMOST’ RECIPROCAL POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 03 May 2018, pp. 70-76
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
A NOTE ON A COMPLETE SOLUTION OF A PROBLEM POSED BY K. MAHLER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 03 May 2018, pp. 60-63
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
On the zeros of Dirichlet
 $L$ -functions
$L$ -functions
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 14 / 2011
- Published online by Cambridge University Press:
- 01 May 2018, pp. 140-154
-
- Article
-
- You have access
- Export citation
UNIVERSAL MIXED ELLIPTIC MOTIVES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 30 April 2018, pp. 663-766
- Print publication:
- May 2020
-
- Article
- Export citation
A NOTE ON THE ERDŐS–GRAHAM THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 23 April 2018, pp. 363-366
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
UNRAMIFIEDNESS OF GALOIS REPRESENTATIONS ATTACHED TO HILBERT MODULAR FORMS MOD
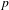 $p$ OF WEIGHT 1
$p$ OF WEIGHT 1
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 23 April 2018, pp. 281-306
- Print publication:
- March 2020
-
- Article
- Export citation
INEQUALITIES ASSOCIATED WITH RATIOS OF GAMMA FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 23 April 2018, pp. 453-458
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
A p-ADIC HERMITIAN MAASS LIFT
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 17 April 2018, pp. 85-114
- Print publication:
- January 2019
-
- Article
-
- You have access
- Export citation
A BOUND FOR THE INDEX OF A QUADRATIC FORM AFTER SCALAR EXTENSION TO THE FUNCTION FIELD OF A QUADRIC
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 16 April 2018, pp. 421-450
- Print publication:
- March 2020
-
- Article
- Export citation
Sums of three squares and Noether–Lefschetz loci
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 5 / May 2018
- Published online by Cambridge University Press:
- 03 April 2018, pp. 1048-1065
- Print publication:
- May 2018
-
- Article
- Export citation
A mass transference principle for systems of linear forms and its applications
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 5 / May 2018
- Published online by Cambridge University Press:
- 03 April 2018, pp. 1014-1047
- Print publication:
- May 2018
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EPSTEIN ZETA-FUNCTIONS, SUBCONVEXITY, AND THE PURITY CONJECTURE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 02 April 2018, pp. 581-596
- Print publication:
- March 2020
-
- Article
- Export citation
IMPROVING AN INEQUALITY FOR THE DIVISOR FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 374-381
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
A VARIATION ON THE THEME OF NICOMACHUS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 367-373
- Print publication:
- June 2018
-
- Article
-
- You have access
- Open access
- Export citation
ON THE GROWTH OF TORSION IN THE COHOMOLOGY OF ARITHMETIC GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 21 March 2018, pp. 537-569
- Print publication:
- March 2020
-
- Article
- Export citation
Abelian varieties isogenous to a power of an elliptic curve
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 5 / May 2018
- Published online by Cambridge University Press:
- 21 March 2018, pp. 934-959
- Print publication:
- May 2018
-
- Article
- Export citation