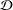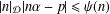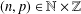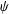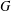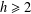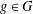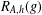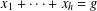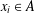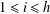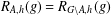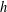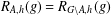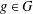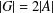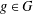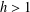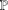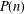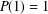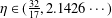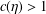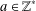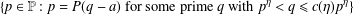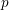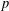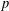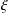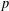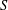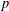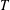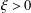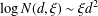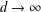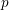Refine listing
Actions for selected content:
2813 results in 11xxx
A GENERALIZATION OF THE RAMANUJAN–NAGELL EQUATION
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 22 August 2018, pp. 535-544
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
SOME REFINED RESULTS ON THE MIXED LITTLEWOOD CONJECTURE FOR PSEUDO-ABSOLUTE VALUES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 22 August 2018, pp. 91-109
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
Distribution of Class Numbers in Continued Fraction Families of Real Quadratic Fields
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 20 August 2018, pp. 1193-1212
-
- Article
- Export citation
REPRESENTATION FUNCTIONS ON ABELIAN GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 15 August 2018, pp. 10-14
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
ON VALUES TAKEN BY THE LARGEST PRIME FACTOR OF SHIFTED PRIMES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 15 August 2018, pp. 133-144
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
ON THE ABSENCE OF ZEROS IN INFINITE ARITHMETIC PROGRESSION FORCERTAIN ZETA FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 15 August 2018, pp. 376-382
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
NOTE ON THE NUMBER OF DIVISORS OF REDUCIBLE QUADRATIC POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 15 August 2018, pp. 1-9
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
CONTINUITY OF ROOTS, REVISITED
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 15 August 2018, pp. 448-455
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
On the General Solution of the Heideman–Hogan Family of Recurrences
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 14 August 2018, pp. 1113-1125
-
- Article
- Export citation
Applications of the hyperbolic Ax–Schanuel conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 9 / September 2018
- Published online by Cambridge University Press:
- 13 August 2018, pp. 1843-1888
- Print publication:
- September 2018
-
- Article
- Export citation
The Manin constant in the semistable case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 9 / September 2018
- Published online by Cambridge University Press:
- 13 August 2018, pp. 1889-1920
- Print publication:
- September 2018
-
- Article
- Export citation
Bounding the Number of Common Zeros of Multivariate Polynomials and Their Consecutive Derivatives
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 2 / March 2019
- Published online by Cambridge University Press:
- 03 August 2018, pp. 253-279
-
- Article
- Export citation
Limit Shapes via Bijections
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 2 / March 2019
- Published online by Cambridge University Press:
- 02 August 2018, pp. 187-240
-
- Article
- Export citation
ON MAHLER’S CLASSIFICATION OF
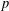 $p$-ADIC NUMBERS
$p$-ADIC NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 30 July 2018, pp. 203-211
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
SINGULARITIES OF THE BIEXTENSION METRIC FOR FAMILIES OF ABELIAN VARIETIES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 23 July 2018, e12
-
- Article
-
- You have access
- Open access
- Export citation
SOME HYPERGEOMETRIC INTEGRALS FOR LINEAR FORMS IN ZETA VALUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 19 July 2018, pp. 372-375
- Print publication:
- December 2018
-
- Article
-
- You have access
- Open access
- Export citation
COMPARING THE BRAUER GROUP TO THE TATE–SHAFAREVICH GROUP
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 19 July 2018, pp. 965-970
- Print publication:
- May 2020
-
- Article
- Export citation
Finiteness theorems for K3 surfaces and abelian varieties of CM type
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 8 / August 2018
- Published online by Cambridge University Press:
- 18 July 2018, pp. 1571-1592
- Print publication:
- August 2018
-
- Article
- Export citation
ALGEBRAIC NUMBERS WITH BOUNDED DEGREE AND WEIL HEIGHT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 18 July 2018, pp. 212-220
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
INTERTWINING SEMISIMPLE CHARACTERS FOR
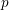 $p$-ADIC CLASSICAL GROUPS
$p$-ADIC CLASSICAL GROUPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 238 / June 2020
- Published online by Cambridge University Press:
- 16 July 2018, pp. 137-205
- Print publication:
- June 2020
-
- Article
-
- You have access
- HTML
- Export citation