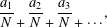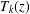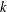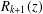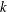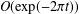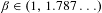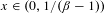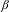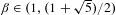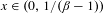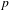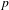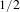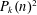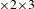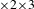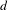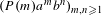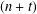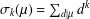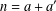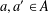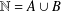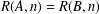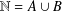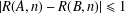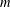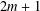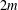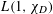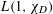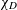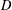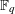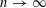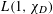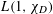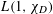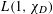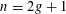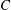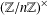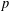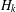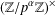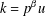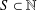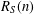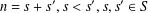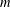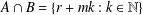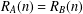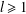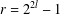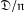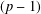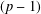Refine listing
Actions for selected content:
2814 results in 11xxx
GENERALIZED CONTINUED FRACTION EXPANSIONS WITH CONSTANT PARTIAL DENOMINATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 21 December 2018, pp. 272-288
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
ON SOME NEW MOCK THETA FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 21 December 2018, pp. 53-66
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
ON THE ACCURACY OF ASYMPTOTIC APPROXIMATIONS TO THE LOG-GAMMA AND RIEMANN–SIEGEL THETA FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 21 December 2018, pp. 319-337
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
DUALITY FOR COHOMOLOGY OF CURVES WITH COEFFICIENTS IN ABELIAN VARIETIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 240 / December 2020
- Published online by Cambridge University Press:
- 19 December 2018, pp. 42-149
- Print publication:
- December 2020
-
- Article
- Export citation
Digit frequencies and self-affine sets with non-empty interior
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 7 / July 2020
- Published online by Cambridge University Press:
- 19 December 2018, pp. 1755-1787
- Print publication:
- July 2020
-
- Article
- Export citation
SECOND MOMENTS IN THE GENERALIZEDGAUSS CIRCLE PROBLEM
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 19 December 2018, e24
-
- Article
-
- You have access
- Open access
- Export citation
A polynomial-exponential variation of Furstenberg’s
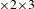 $\times 2\times 3$ theorem
$\times 2\times 3$ theorem
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 7 / July 2020
- Published online by Cambridge University Press:
- 19 December 2018, pp. 1729-1737
- Print publication:
- July 2020
-
- Article
- Export citation
AN ANALOGUE OF EULER’S IDENTITY AND SPLIT PERFECT PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 17 December 2018, pp. 353-361
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Approximating the Riemann Zeta-function by Polynomials with Restricted Zeros
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 17 December 2018, pp. 475-478
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
ON PARTITIONS OF NONNEGATIVE INTEGERS AND REPRESENTATION FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 11 December 2018, pp. 385-387
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
COMPLETENESS OF THE LIST OF SPINOR REGULAR TERNARY QUADRATIC FORMS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 2 / 2019
- Published online by Cambridge University Press:
- 05 December 2018, pp. 213-235
- Print publication:
- 2019
-
- Article
- Export citation
COMPLEX MOMENTS AND THE DISTRIBUTION OF VALUES OF
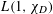 $L(1,\unicode[STIX]{x1D712}_{D})$ OVER FUNCTION FIELDS WITH APPLICATIONS TO CLASS NUMBERS
$L(1,\unicode[STIX]{x1D712}_{D})$ OVER FUNCTION FIELDS WITH APPLICATIONS TO CLASS NUMBERS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 2 / 2019
- Published online by Cambridge University Press:
- 05 December 2018, pp. 236-271
- Print publication:
- 2019
-
- Article
- Export citation
On the Frequency of Algebraic Brauer Classes on Certain Log K3 Surfaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 03 December 2018, pp. 551-563
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
Numbers with Almost all Convergents in a Cantor Set
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 03 December 2018, pp. 869-875
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
ZERO-LOCI OF BRAUER GROUP ELEMENTS ON SEMI-SIMPLE ALGEBRAIC GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 5 / September 2020
- Published online by Cambridge University Press:
- 29 November 2018, pp. 1467-1507
- Print publication:
- September 2020
-
- Article
- Export citation
Metrical Results on the Distribution of Fractional Parts of Powers of Real Numbers
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 29 November 2018, pp. 505-521
-
- Article
- Export citation
A NEW MENON’S IDENTITY FROM GROUP ACTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 28 November 2018, pp. 369-375
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
ON A PROBLEM OF CHEN AND LEV
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 28 November 2018, pp. 15-22
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
IDEAL CHAINS IN RESIDUALLY FINITE DEDEKIND DOMAINS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 28 November 2018, pp. 56-67
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
CONGRUENCES FOR THE
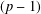 $(p-1)$TH APÉRY NUMBER
$(p-1)$TH APÉRY NUMBER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 28 November 2018, pp. 362-368
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation