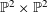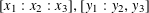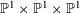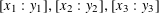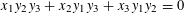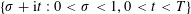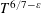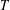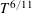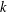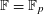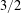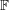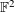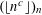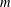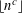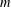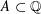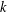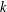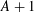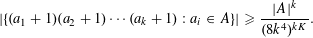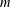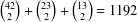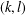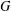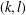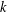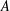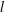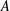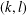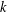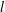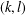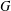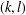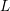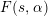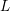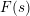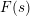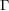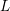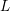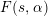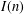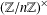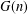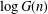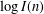Refine listing
Actions for selected content:
2812 results in 11xxx
THE POWER-SAVING MANIN–PEYRE CONJECTURE FOR A SENARY CUBIC
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 4 / 2019
- Published online by Cambridge University Press:
- 22 May 2019, pp. 789-830
- Print publication:
- 2019
-
- Article
- Export citation
ON SIMPLE ZEROS OF THE DEDEKIND ZETA-FUNCTION OF A QUADRATIC NUMBER FIELD
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 4 / 2019
- Published online by Cambridge University Press:
- 22 May 2019, pp. 851-861
- Print publication:
- 2019
-
- Article
- Export citation
DENSITY OF POWER-FREE VALUES OF POLYNOMIALS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 4 / 2019
- Published online by Cambridge University Press:
- 14 August 2019, pp. 1038-1050
- Print publication:
- 2019
-
- Article
- Export citation
NEW RESULTS ON SUM-PRODUCT TYPE GROWTH OVER FIELDS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 02 April 2019, pp. 588-642
- Print publication:
- 2019
-
- Article
- Export citation
RANDOMNESS AND NON-RANDOMNESS PROPERTIES OF PIATETSKI-SHAPIRO SEQUENCES MODULO
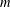 $m$
$m$
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 4 / 2019
- Published online by Cambridge University Press:
- 14 August 2019, pp. 1051-1073
- Print publication:
- 2019
-
- Article
- Export citation
ON ITERATED PRODUCT SETS WITH SHIFTS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 4 / 2019
- Published online by Cambridge University Press:
- 21 May 2019, pp. 831-850
- Print publication:
- 2019
-
- Article
- Export citation
LONELY RUNNERS IN FUNCTION FIELDS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 12 April 2019, pp. 677-701
- Print publication:
- 2019
-
- Article
- Export citation
Mean values of derivatives of L-functions in function fields: III
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 905-913
- Print publication:
- August 2019
-
- Article
- Export citation
A NOTE ON THE EQUIVALENCE OF THE PARITY OF CLASS NUMBERS AND THE SIGNATURE RANKS OF UNITS IN CYCLOTOMIC FIELDS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 238 / June 2020
- Published online by Cambridge University Press:
- 27 December 2018, pp. 206-214
- Print publication:
- June 2020
-
- Article
-
- You have access
- HTML
- Export citation
ON FINDING SOLUTIONS TO EXPONENTIAL CONGRUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 388-391
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
HYPERGEOMETRIC MODULAR EQUATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 338-366
- Print publication:
- December 2019
-
- Article
-
- You have access
- Open access
- Export citation
Pólya S3-extensions of ℚ
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 1421-1433
- Print publication:
- December 2019
-
- Article
- Export citation
A problem of integer partitions and numerical semigroups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 969-978
- Print publication:
- August 2019
-
- Article
- Export citation
THE MAXIMUM SIZE OF
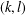 $(k,l)$-SUM-FREE SETS IN CYCLIC GROUPS
$(k,l)$-SUM-FREE SETS IN CYCLIC GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 26 December 2018, pp. 184-194
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
ANALOGUES OF THE AOKI–OHNO AND LE–MURAKAMI RELATIONS FOR FINITE MULTIPLE ZETA VALUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 26 December 2018, pp. 34-40
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
HASSE PRINCIPLES FOR ÉTALE MOTIVIC COHOMOLOGY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 236 / December 2019
- Published online by Cambridge University Press:
- 26 December 2018, pp. 63-83
- Print publication:
- December 2019
-
- Article
-
- You have access
- HTML
- Export citation
ON THE STANDARD TWIST OF THE
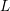 $L$-FUNCTIONS OF HALF-INTEGRAL WEIGHT CUSP FORMS
$L$-FUNCTIONS OF HALF-INTEGRAL WEIGHT CUSP FORMS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 240 / December 2020
- Published online by Cambridge University Press:
- 26 December 2018, pp. 150-180
- Print publication:
- December 2020
-
- Article
- Export citation
THE DISTRIBUTION OF THE NUMBER OF SUBGROUPS OF THE MULTIPLICATIVE GROUP
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 21 December 2018, pp. 46-97
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
GENERALIZED CONTINUED FRACTION EXPANSIONS WITH CONSTANT PARTIAL DENOMINATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 21 December 2018, pp. 272-288
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
ON SOME NEW MOCK THETA FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 21 December 2018, pp. 53-66
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation