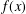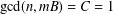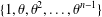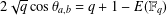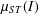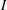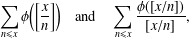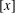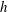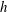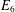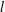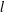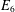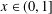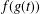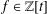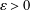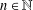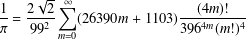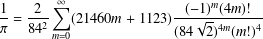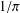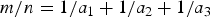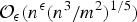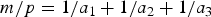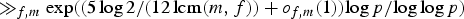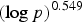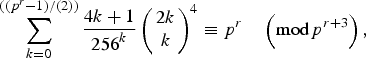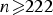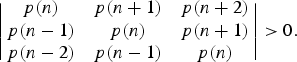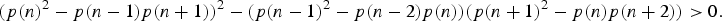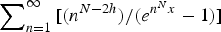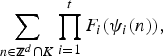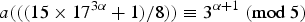Refine listing
Actions for selected content:
2812 results in 11xxx
ON THE DISTRIBUTION OF THE RANK STATISTIC FOR STRONGLY CONCAVE COMPOSITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 13 February 2019, pp. 230-238
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
A BRIEF NOTE ON SOME INFINITE FAMILIES OF MONOGENIC POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 13 February 2019, pp. 239-244
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
Persistent Hall rays for Lagrange spectra at cusps of Riemann surfaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 11 February 2019, pp. 2017-2072
- Print publication:
- August 2020
-
- Article
- Export citation
On the Schertz Conjecture
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 08 February 2019, pp. 837-845
-
- Article
- Export citation
THE ERROR TERM IN THE SATO–TATE THEOREM OF BIRCH
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 08 February 2019, pp. 27-33
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
NOTE ON SUMS INVOLVING THE EULER FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 07 February 2019, pp. 194-200
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
Zeroes of Polynomials With Prime Inputs and Schmidt’s
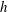 $h$-invariant
$h$-invariant
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 07 February 2019, pp. 805-833
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
COMPATIBLE SYSTEMS OF GALOIS REPRESENTATIONS ASSOCIATED TO THE EXCEPTIONAL GROUP
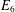 $E_{6}$
$E_{6}$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 06 February 2019, e4
-
- Article
-
- You have access
- Open access
- Export citation
A NOTE ON THE INTERSECTIONS OF THE BESICOVITCH SETS AND ERDŐS–RÉNYI SETS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 01 February 2019, pp. 33-45
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
SMOOTH VALUES OF POLYNOMIALS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 01 February 2019, pp. 245-261
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
A MODULAR PROOF OF TWO OF RAMANUJAN’S FORMULAE FOR
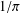 $1/\unicode[STIX]{x1D70B}$
$1/\unicode[STIX]{x1D70B}$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 01 February 2019, pp. 131-144
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
The number of solutions of the Erdős-Straus Equation and sums of k unit fractions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 1401-1427
- Print publication:
- June 2020
-
- Article
- Export citation
Some congruences involving fourth powers of central q-binomial coefficients
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 1127-1138
- Print publication:
- June 2020
-
- Article
- Export citation
Explicit Salem sets, Fourier restriction, and metric Diophantine approximation in the p-adic numbers
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 1265-1288
- Print publication:
- June 2020
-
- Article
- Export citation
Determinantal inequalities for the partition function
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 1451-1466
- Print publication:
- June 2020
-
- Article
- Export citation
Generalized Lambert series and arithmetic nature of odd zeta values
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 24 January 2019, pp. 741-769
- Print publication:
- April 2020
-
- Article
- Export citation
Binary quadratic forms and ray class groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 23 January 2019, pp. 695-720
- Print publication:
- April 2020
-
- Article
- Export citation
Explicit asymptotics for certain single and double exponential sums
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 22 January 2019, pp. 607-632
- Print publication:
- April 2020
-
- Article
- Export citation
Asymptotics for some polynomial patterns in the primes
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 17 January 2019, pp. 1241-1290
- Print publication:
- October 2019
-
- Article
- Export citation
Infinite families of congruences modulo 5 and 7 for the cubic partition function
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1189-1205
- Print publication:
- October 2019
-
- Article
- Export citation