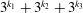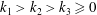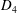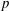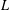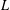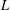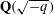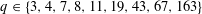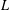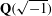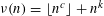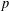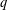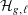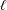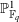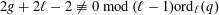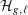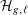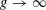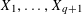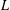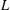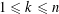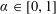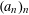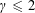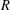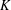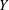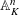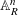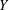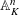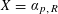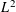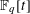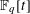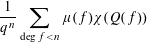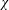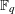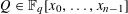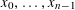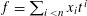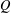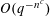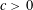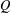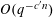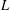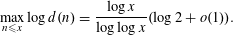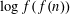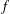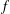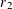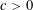Refine listing
Actions for selected content:
2812 results in 11xxx
The Hermite–Joubert Problem and a Conjecture of Brassil and Reichstein
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 04 January 2019, pp. 169-177
- Print publication:
- March 2019
-
- Article
-
- You have access
- Export citation
Irregular Weight One Points with
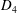 $D_{4}$ Image
$D_{4}$ Image
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 04 January 2019, pp. 109-118
- Print publication:
- March 2019
-
- Article
-
- You have access
- Export citation
A CONVERSE THEOREM WITHOUT ROOT NUMBERS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 4 / 2019
- Published online by Cambridge University Press:
- 21 May 2019, pp. 862-873
- Print publication:
- 2019
-
- Article
- Export citation
QUANTITATIVE ESTIMATES FOR SIMPLE ZEROS OF
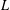 $L$-FUNCTIONS
$L$-FUNCTIONS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 2 / 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 375-399
- Print publication:
- 2019
-
- Article
- Export citation
CLASS NUMBER ONE FROM ANALYTIC RANK TWO
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 2 / 2019
- Published online by Cambridge University Press:
- 03 January 2019, pp. 333-374
- Print publication:
- 2019
-
- Article
- Export citation
MULTIDIMENSIONAL VAN DER CORPUT SETS AND SMALL FRACTIONAL PARTS OF POLYNOMIALS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 2 / 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 400-435
- Print publication:
- 2019
-
- Article
- Export citation
ON THE DISTRIBUTION OF THE RATIONAL POINTS ON CYCLIC COVERS IN THE ABSENCE OF ROOTS OF UNITY
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 17 April 2019, pp. 719-742
- Print publication:
- 2019
-
- Article
- Export citation
ON A TWISTED VERSION OF LINNIK AND SELBERG’S CONJECTURE ON SUMS OF KLOOSTERMAN SUMS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 29 January 2019, pp. 437-474
- Print publication:
- 2019
-
- Article
- Export citation
A MEAN VALUE RESULT FOR A PRODUCT OF GL(2) AND GL(3)
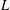 $L$-FUNCTIONS
$L$-FUNCTIONS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 17 April 2019, pp. 743-762
- Print publication:
- 2019
-
- Article
- Export citation
A CLASS OF IRREDUCIBLE POLYNOMIALS ASSOCIATED WITH PRIME DIVISORS OF VALUES OF CYCLOTOMIC POLYNOMIALS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 4 / 2019
- Published online by Cambridge University Press:
- 14 August 2019, pp. 1033-1037
- Print publication:
- 2019
-
- Article
- Export citation
HADAMARD MATRICES AND 1-FACTORIZATIONS OF COMPLETE GRAPHS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 11 February 2019, pp. 488-499
- Print publication:
- 2019
-
- Article
- Export citation
THERE IS NO KHINTCHINE THRESHOLD FOR METRIC PAIR CORRELATIONS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 4 / 2019
- Published online by Cambridge University Press:
- 23 July 2019, pp. 929-949
- Print publication:
- 2019
-
- Article
- Export citation
INTERVALS BETWEEN CONSECUTIVE NUMBERS WHICH ARE SUMS OF TWO SQUARES
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 4 / 2019
- Published online by Cambridge University Press:
- 14 August 2019, pp. 1018-1032
- Print publication:
- 2019
-
- Article
- Export citation
MODELS OF TORSORS OVER AFFINE SPACES
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 07 March 2019, pp. 530-541
- Print publication:
- 2019
-
- Article
- Export citation
CANCELLATIONS BETWEEN KLOOSTERMAN SUMS MODULO A PRIME POWER WITH PRIME ARGUMENTS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 29 January 2019, pp. 475-487
- Print publication:
- 2019
-
- Article
- Export citation
CENTRAL LIMIT THEOREM FOR PLANCK-SCALE MASS DISTRIBUTION OF TORAL LAPLACE EIGENFUNCTIONS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 12 April 2019, pp. 643-676
- Print publication:
- 2019
-
- Article
- Export citation
LINEAR AND QUADRATIC UNIFORMITY OF THE MÖBIUS FUNCTION OVER
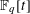 $\mathbb{F}_{q}[t]$
$\mathbb{F}_{q}[t]$
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 05 March 2019, pp. 505-529
- Print publication:
- 2019
-
- Article
- Export citation
A CERTAIN DIRICHLET SERIES OF RANKIN–SELBERG TYPE ASSOCIATED WITH THE IKEDA LIFT OF HALF-INTEGRAL WEIGHT
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 4 / 2019
- Published online by Cambridge University Press:
- 17 June 2019, pp. 897-928
- Print publication:
- 2019
-
- Article
- Export citation
POINT DISTRIBUTIONS IN TWO-POINT HOMOGENEOUS SPACES
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 26 March 2019, pp. 557-587
- Print publication:
- 2019
-
- Article
- Export citation
THE MAXIMAL ORDER OF ITERATED MULTIPLICATIVE FUNCTIONS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 4 / 2019
- Published online by Cambridge University Press:
- 30 July 2019, pp. 990-1009
- Print publication:
- 2019
-
- Article
- Export citation