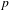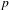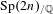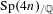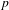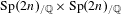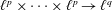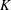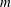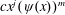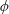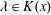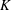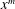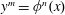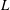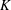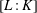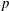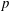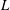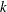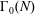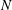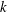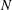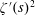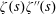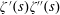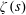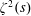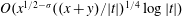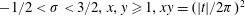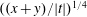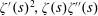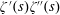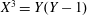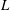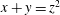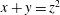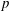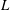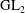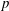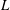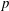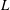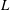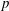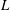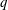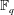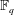Refine listing
Actions for selected content:
2812 results in 11xxx
Diophantine approximation on the parabola with non-monotonic approximation functions
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 168 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 15 January 2019, pp. 535-542
- Print publication:
- May 2020
-
- Article
- Export citation
The fifth moment of Hecke L-functions in the weight aspect
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 168 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 14 January 2019, pp. 543-566
- Print publication:
- May 2020
-
- Article
- Export citation
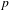 $p$-ADIC
$p$-ADIC  $L$-FUNCTIONS FOR ORDINARY FAMILIES ON SYMPLECTIC GROUPS
$L$-FUNCTIONS FOR ORDINARY FAMILIES ON SYMPLECTIC GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 14 January 2019, pp. 1287-1347
- Print publication:
- July 2020
-
- Article
- Export citation
Discrete Multilinear Spherical Averages
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 243-246
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Powers in Orbits of Rational Functions: Cases of an Arithmetic Dynamical Mordell–Lang Conjecture
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 773-817
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
Annihilators of the Ideal Class Group of a Cyclic Extension of an Imaginary Quadratic Field
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 1395-1419
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Eisenstein Series Arising from Jordan Algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 09 January 2019, pp. 183-201
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
Factorization Tests and Algorithms Arising from Counting Modular Forms and Automorphic Representations
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 81-97
- Print publication:
- March 2019
-
- Article
-
- You have access
- Export citation
Titchmarsh’s Method for the Approximate Functional Equations for
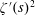 $\unicode[STIX]{x1D701}^{\prime }(s)^{2}$,
$\unicode[STIX]{x1D701}^{\prime }(s)^{2}$, 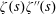 $\unicode[STIX]{x1D701}(s)\unicode[STIX]{x1D701}^{\prime \prime }(s)$, and
$\unicode[STIX]{x1D701}(s)\unicode[STIX]{x1D701}^{\prime \prime }(s)$, and 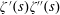 $\unicode[STIX]{x1D701}^{\prime }(s)\unicode[STIX]{x1D701}^{\prime \prime }(s)$
$\unicode[STIX]{x1D701}^{\prime }(s)\unicode[STIX]{x1D701}^{\prime \prime }(s)$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 1465-1493
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Cubic Twin Prime Polynomials are Counted by a Modular Form
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 1323-1350
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Logarithmes des points rationnels des variétés abéliennes
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 247-298
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
Cohomological Approach to Class Field Theory in Arithmetic Topology
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 891-935
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
Weighted Distribution of Low-lying Zeros of GL(2)
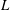 $L$-functions
$L$-functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 08 January 2019, pp. 153-182
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
Monochromatic Solutions to
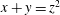 $x+y=z^{2}$
$x+y=z^{2}$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 579-605
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Sharp Bertini Theorem for Plane Curves over Finite Fields
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 223-230
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Models of Representations and Langlands Functoriality
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 07 January 2019, pp. 676-707
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
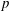 $p$-adic
$p$-adic 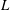 $L$-functions for
$L$-functions for 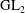 $\text{GL}_{2}$
$\text{GL}_{2}$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 1019-1059
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
Irreducible Polynomials Over a Finite Field with Restricted Coefficients
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 429-439
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
On the geometry and regularity of invariant sets of piecewise-affine automorphisms on the Euclidean space
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 07 January 2019, pp. 2183-2218
- Print publication:
- August 2020
-
- Article
- Export citation
One Level Density for Cubic Galois Number Fields
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 04 January 2019, pp. 149-167
- Print publication:
- March 2019
-
- Article
-
- You have access
- Export citation