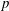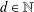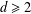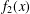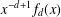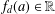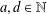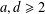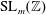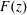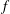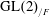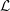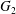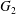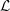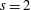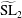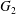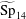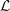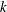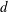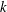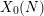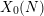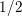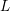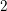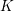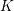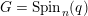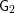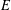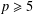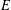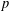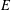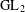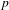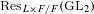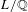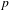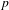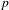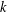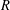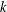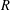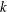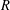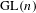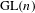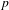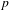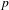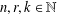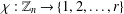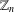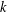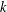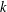Refine listing
Actions for selected content:
2812 results in 11xxx
HOW SMALL CAN POLYNOMIALS BE IN AN INTERVAL OF GIVEN LENGTH?
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 13 March 2019, pp. 261-280
- Print publication:
- May 2020
-
- Article
-
- You have access
- Export citation
Local Shtukas and Divisible Local Anderson Modules
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 12 March 2019, pp. 1163-1207
- Print publication:
- October 2019
-
- Article
-
- You have access
- Open access
- Export citation
ON GENERALIZED THUE–MORSE FUNCTIONS AND THEIR VALUES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 11 March 2019, pp. 177-201
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
The Bombieri–Vinogradov Theorem on Higher Rank Groups and its Applications
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 07 March 2019, pp. 928-966
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Ramification of the Eigencurve at Classical RM Points
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 07 March 2019, pp. 57-88
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
Poles of the Standard
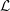 ${\mathcal{L}}$-function of
${\mathcal{L}}$-function of 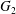 $G_{2}$ and the Rallis–Schiffmann Lift
$G_{2}$ and the Rallis–Schiffmann Lift
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 07 March 2019, pp. 1127-1161
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
Eigenvalue Optimisation on Flat Tori and Lattice Points in Anisotropically Expanding Domains
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 07 March 2019, pp. 967-987
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
A CONVERSE THEOREM FOR BORCHERDS PRODUCTS ON
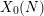 $X_{0}(N)$
$X_{0}(N)$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 240 / December 2020
- Published online by Cambridge University Press:
- 01 March 2019, pp. 237-256
- Print publication:
- December 2020
-
- Article
- Export citation
Spinor groups with good reduction
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 3 / March 2019
- Published online by Cambridge University Press:
- 07 March 2019, pp. 484-527
- Print publication:
- March 2019
-
- Article
- Export citation
On the multifractal analysis of the covering number on the Galton–Watson tree
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 12 July 2019, pp. 265-281
- Print publication:
- March 2019
-
- Article
- Export citation
ON THE SELMER GROUP OF A CERTAIN
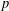 $p$-ADIC LIE EXTENSION
$p$-ADIC LIE EXTENSION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 27 February 2019, pp. 245-255
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
A LOWER BOUND FOR THE LARGE SIEVE WITH SQUARE MODULI
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 27 February 2019, pp. 225-229
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
TWISTED TRIPLE PRODUCT
 $\text{p}$-ADIC L-FUNCTIONS AND HIRZEBRUCH–ZAGIER CYCLES
$\text{p}$-ADIC L-FUNCTIONS AND HIRZEBRUCH–ZAGIER CYCLES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 20 February 2019, pp. 1947-1992
- Print publication:
- November 2020
-
- Article
- Export citation
FACTORS OF CARMICHAEL NUMBERS AND AN EVEN WEAKER
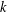 $k$-TUPLES CONJECTURE
$k$-TUPLES CONJECTURE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 20 February 2019, pp. 376-384
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
NONNEGATIVE MULTIPLICATIVE FUNCTIONS ON SIFTED SETS, AND THE SQUARE ROOTS OF −1 MODULO SHIFTED PRIMES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 20 February 2019, pp. 187-199
- Print publication:
- January 2020
-
- Article
-
- You have access
- Export citation
ON THE TRANSCENDENCE OF CERTAIN REAL NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 20 February 2019, pp. 392-402
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
PARITY OF THE LANGLANDS PARAMETERS OF CONJUGATE SELF-DUAL REPRESENTATIONS OF
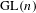 $\text{GL}(n)$ AND THE LOCAL JACQUET–LANGLANDS CORRESPONDENCE
$\text{GL}(n)$ AND THE LOCAL JACQUET–LANGLANDS CORRESPONDENCE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 19 February 2019, pp. 2017-2043
- Print publication:
- November 2020
-
- Article
- Export citation
ON THE
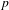 $p$-ADIC VARIATION OF HEEGNER POINTS
$p$-ADIC VARIATION OF HEEGNER POINTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 18 February 2019, pp. 2127-2164
- Print publication:
- November 2020
-
- Article
- Export citation
A MAGNETIC DOUBLE INTEGRAL
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 18 February 2019, pp. 9-25
- Print publication:
- August 2019
-
- Article
-
- You have access
- Open access
- Export citation
ALTERNATING COLOURINGS OF THE VERTICES OF A REGULAR POLYGON
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 13 February 2019, pp. 177-181
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation