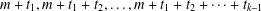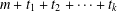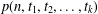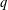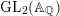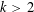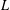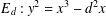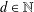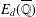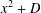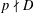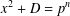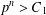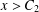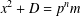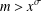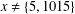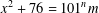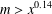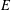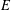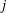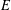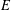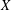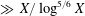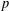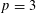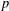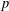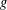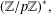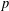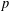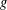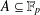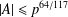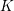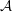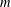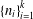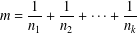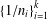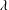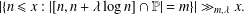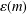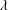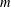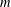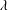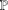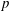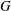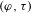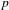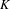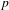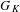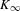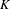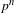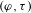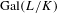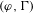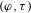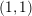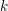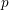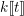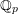Refine listing
Actions for selected content:
2812 results in 11xxx
PARTITIONS WITH AN ARBITRARY NUMBER OF SPECIFIED DISTANCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 03 June 2019, pp. 35-39
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
Simple zeros of automorphic
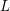 $L$-functions
$L$-functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 6 / June 2019
- Published online by Cambridge University Press:
- 30 May 2019, pp. 1224-1243
- Print publication:
- June 2019
-
- Article
- Export citation
A PROOF OF ANDREWS’ CONJECTURE ON PARTITIONS WITH NO SHORT SEQUENCES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 30 May 2019, e17
-
- Article
-
- You have access
- Open access
- Export citation
ON A NONCRITICAL SYMMETRIC SQUARE
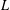 $L$-VALUE OF THE CONGRUENT NUMBER ELLIPTIC CURVES
$L$-VALUE OF THE CONGRUENT NUMBER ELLIPTIC CURVES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 27 May 2019, pp. 13-22
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
ON THE FACTORISATION OF
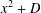 $x^{2}+D$
$x^{2}+D$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 27 May 2019, pp. 206-215
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
ENLARGED MIXED SHIMURA VARIETIES, BI-ALGEBRAIC SYSTEM AND SOME AX TYPE TRANSCENDENTAL RESULTS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 27 May 2019, e16
-
- Article
-
- You have access
- Open access
- Export citation
GOLDFELD’S CONJECTURE AND CONGRUENCES BETWEEN HEEGNER POINTS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 27 May 2019, e15
-
- Article
-
- You have access
- Open access
- Export citation
PRIMES IN ARITHMETIC PROGRESSIONS AND NONPRIMITIVE ROOTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 24 May 2019, pp. 388-394
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
A NEW SUM–PRODUCT ESTIMATE IN PRIME FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 24 May 2019, pp. 268-280
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
On the Discriminants of the Powers of an Algebraic Integer
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 22 May 2019, pp. 481-483
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
CLASS NUMBER FORMULA FOR DIHEDRAL EXTENSIONS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 21 May 2019, pp. 323-353
- Print publication:
- May 2020
-
- Article
-
- You have access
- Export citation
Local-global principles in circle packings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 6 / June 2019
- Published online by Cambridge University Press:
- 20 May 2019, pp. 1118-1170
- Print publication:
- June 2019
-
- Article
- Export citation
A NOTE ON THE SUM OF RECIPROCALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 17 May 2019, pp. 189-193
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
POSITIVE PROPORTION OF SHORT INTERVALS CONTAINING A PRESCRIBED NUMBER OF PRIMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 17 May 2019, pp. 378-387
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
THE NUMBER OF CYCLIC SUBGROUPS OF FINITE ABELIAN GROUPS AND MENON’S IDENTITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 17 May 2019, pp. 201-206
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
An effective Chabauty–Kim theorem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 6 / June 2019
- Published online by Cambridge University Press:
- 14 May 2019, pp. 1057-1075
- Print publication:
- June 2019
-
- Article
- Export citation
Primes Dividing Invariants of CM Picard Curves
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 07 May 2019, pp. 480-504
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
On Some Generalized Rapoport–Zink Spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 03 May 2019, pp. 1111-1187
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
LOCALLY ANALYTIC VECTORS AND OVERCONVERGENT
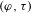 $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D70F})$-MODULES
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D70F})$-MODULES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 03 May 2019, pp. 137-185
- Print publication:
- January 2021
-
- Article
- Export citation
Cycle classes in overconvergent rigid cohomology and a semistable Lefschetz
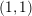 $(1,1)$ theorem
$(1,1)$ theorem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 5 / May 2019
- Published online by Cambridge University Press:
- 02 May 2019, pp. 1025-1045
- Print publication:
- May 2019
-
- Article
- Export citation