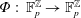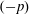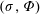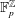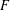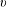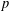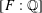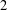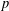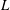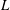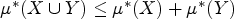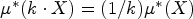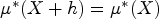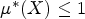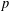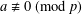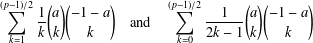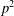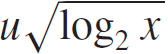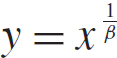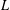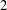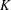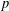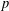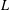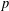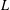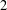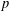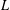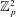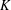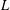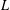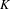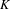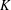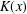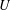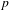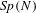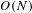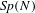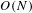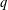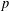Refine listing
Actions for selected content:
2812 results in 11xxx
Automaticity and Invariant Measures of Linear Cellular Automata
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 05 September 2019, pp. 1691-1726
- Print publication:
- December 2020
-
- Article
- Export citation
PARALLEL WEIGHT 2 POINTS ON HILBERT MODULAR EIGENVARIETIES AND THE PARITY CONJECTURE
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 04 September 2019, e27
-
- Article
-
- You have access
- Open access
- Export citation
One-Level Density of Low-lying Zeros of Quadratic and Quartic Hecke
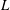 $L$-functions
$L$-functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 30 August 2019, pp. 427-454
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
On the notions of upper and lower density
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 30 August 2019, pp. 139-167
-
- Article
- Export citation
NEW SUPERCONGRUENCES INVOLVING PRODUCTS OF TWO BINOMIAL COEFFICIENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 23 August 2019, pp. 367-378
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
ON LITTLEWOOD’S PROOF OF THE PRIME NUMBER THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 15 August 2019, pp. 226-232
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
On the bivariate Erdős–Kac theorem and correlations of the Möbius function
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 3 / November 2020
- Published online by Cambridge University Press:
- 14 August 2019, pp. 547-605
- Print publication:
- November 2020
-
- Article
- Export citation
CODIMENSION TWO CYCLES IN IWASAWA THEORY AND ELLIPTIC CURVES WITH SUPERSINGULAR REDUCTION
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 13 August 2019, e25
-
- Article
-
- You have access
- Open access
- Export citation
SATO–TATE EQUIDISTRIBUTION OF CERTAIN FAMILIES OF ARTIN
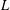 $L$-FUNCTIONS
$L$-FUNCTIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 13 August 2019, e23
-
- Article
-
- You have access
- Open access
- Export citation
HIGHER
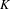 $K$-THEORY OF FORMS I. FROM RINGS TO EXACT CATEGORIES
$K$-THEORY OF FORMS I. FROM RINGS TO EXACT CATEGORIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 4 / July 2021
- Published online by Cambridge University Press:
- 02 August 2019, pp. 1205-1273
- Print publication:
- July 2021
-
- Article
- Export citation
Limiting distributions of translates of divergent diagonal orbits
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 9 / September 2019
- Published online by Cambridge University Press:
- 02 August 2019, pp. 1747-1793
- Print publication:
- September 2019
-
- Article
- Export citation
On some incomplete theta integrals
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 9 / September 2019
- Published online by Cambridge University Press:
- 02 August 2019, pp. 1711-1746
- Print publication:
- September 2019
-
- Article
- Export citation
IGUSA’S CONJECTURE FOR EXPONENTIAL SUMS: OPTIMAL ESTIMATES FOR NONRATIONAL SINGULARITIES
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 7 / 2019
- Published online by Cambridge University Press:
- 31 July 2019, e3
-
- Article
-
- You have access
- Open access
- Export citation
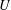 $U$-NUMBERS IN FIELDS OF FORMAL POWER SERIES OVER FINITE FIELDS
$U$-NUMBERS IN FIELDS OF FORMAL POWER SERIES OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 29 July 2019, pp. 218-225
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
A COMBINATORIAL SOLUTION TO MŒGLIN’S PARAMETRIZATION OF ARTHUR PACKETS FOR
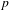 $p$-ADIC QUASISPLIT
$p$-ADIC QUASISPLIT 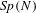 $Sp(N)$ AND
$Sp(N)$ AND 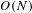 $O(N)$
$O(N)$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 4 / July 2021
- Published online by Cambridge University Press:
- 25 July 2019, pp. 1091-1204
- Print publication:
- July 2021
-
- Article
- Export citation
ON A GENERALISATION OF A RESTRICTED SUM FORMULA FOR MULTIPLE ZETA VALUES AND FINITE MULTIPLE ZETA VALUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 24 July 2019, pp. 23-34
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
GENERALISATION OF A RESULT ON DISTINCT PARTITIONS WITH BOUNDED PART DIFFERENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 24 July 2019, pp. 233-237
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
SYMMETRIC FUNCTIONS AND MULTIPLE ZETA VALUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 24 July 2019, pp. 426-437
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
DEFORMATION CONDITIONS FOR PSEUDOREPRESENTATIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 18 July 2019, e20
-
- Article
-
- You have access
- Open access
- Export citation
A
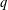 $q$-ANALOGUE OF A HYPERGEOMETRIC CONGRUENCE
$q$-ANALOGUE OF A HYPERGEOMETRIC CONGRUENCE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 18 July 2019, pp. 294-298
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation