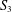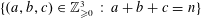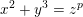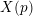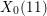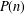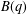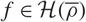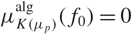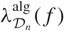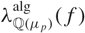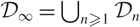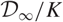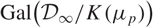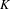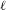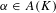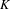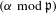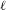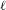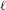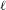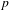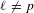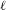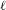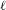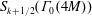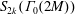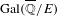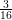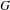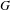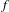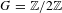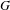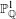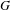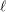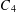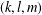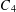Refine listing
Actions for selected content:
2812 results in 11xxx
FINE DELIGNE–LUSZTIG VARIETIES AND ARITHMETIC FUNDAMENTAL LEMMAS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 10 December 2019, e47
-
- Article
-
- You have access
- Open access
- Export citation
A DISTRIBUTION ON TRIPLES WITH MAXIMUM ENTROPY MARGINAL
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 09 December 2019, e46
-
- Article
-
- You have access
- Open access
- Export citation
The generalized Fermat equation with exponents 2, 3,
 $n$
$n$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 26 November 2019, pp. 77-113
- Print publication:
- January 2020
-
- Article
- Export citation
Arithmeticity of the monodromy of some Kodaira fibrations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 26 November 2019, pp. 114-157
- Print publication:
- January 2020
-
- Article
- Export citation
LOWER BOUNDS FOR PERIODS OF DUCCI SEQUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 22 November 2019, pp. 31-38
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
ARITHMETIC PROPERTIES OF COEFFICIENTS OF THE MOCK THETA FUNCTION
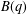 $B(q)$
$B(q)$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 21 November 2019, pp. 50-58
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Variation of the algebraic λ-invariant over a solvable extension
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 21 November 2019, pp. 499-521
- Print publication:
- May 2021
-
- Article
- Export citation
Moments of the Dedekind zeta function and other non-primitive L-functions
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 15 November 2019, pp. 191-219
- Print publication:
- January 2021
-
- Article
- Export citation
REDUCTIONS OF POINTS ON ALGEBRAIC GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 14 November 2019, pp. 1637-1669
- Print publication:
- September 2021
-
- Article
- Export citation
Patching over Berkovich curves and quadratic forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 12 / December 2019
- Published online by Cambridge University Press:
- 11 November 2019, pp. 2399-2438
- Print publication:
- December 2019
-
- Article
- Export citation
THE
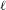 $\ell$-MODULAR LOCAL LANGLANDS CORRESPONDENCE AND LOCAL CONSTANTS
$\ell$-MODULAR LOCAL LANGLANDS CORRESPONDENCE AND LOCAL CONSTANTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 08 November 2019, pp. 1585-1635
- Print publication:
- September 2021
-
- Article
- Export citation
Vinogradov’s three primes theorem with primes having given primitive roots
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 05 November 2019, pp. 75-110
- Print publication:
- January 2021
-
- Article
- Export citation
Newforms of Half-integral Weight: The Minus Space Counterpart
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 31 October 2019, pp. 326-372
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
GALOIS CONJUGATES OF SPECIAL POINTS AND SPECIAL SUBVARIETIES IN SHIMURA VARIETIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 30 October 2019, pp. 1075-1089
- Print publication:
- May 2021
-
- Article
- Export citation
On Selberg’s eigenvalue conjecture for moduli spaces of abelian differentials
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 12 / December 2019
- Published online by Cambridge University Press:
- 30 October 2019, pp. 2354-2398
- Print publication:
- December 2019
-
- Article
- Export citation
DENSITY RESULTS FOR SPECIALIZATION SETS OF GALOIS COVERS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 25 October 2019, pp. 1455-1496
- Print publication:
- September 2021
-
- Article
-
- You have access
- Open access
- Export citation
Compatible systems and ramification
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 12 / December 2019
- Published online by Cambridge University Press:
- 21 October 2019, pp. 2334-2353
- Print publication:
- December 2019
-
- Article
- Export citation
Cotangent Sums Related to the Riemann Hypothesis for Various Shifts of the Argument
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 15 October 2019, pp. 522-535
- Print publication:
- September 2020
-
- Article
-
- You have access
- Open access
- Export citation
PERFECT TRIANGLES ON THE CURVE
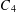 $C_{4}$
$C_{4}$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 09 October 2019, pp. 68-80
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Polylogarithmic bounds in the nilpotent Freiman theorem
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 08 October 2019, pp. 111-127
- Print publication:
- January 2021
-
- Article
- Export citation