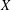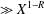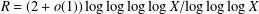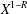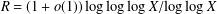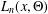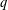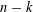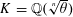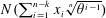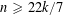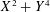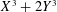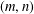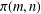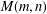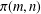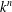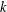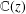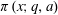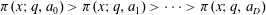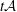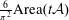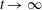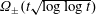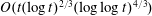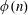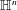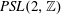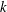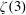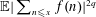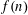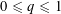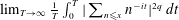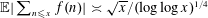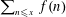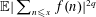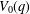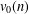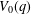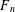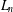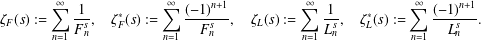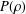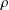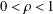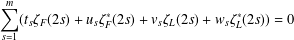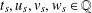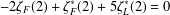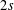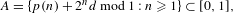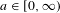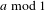Refine listing
Actions for selected content:
2812 results in 11xxx
A CONDITIONAL DENSITY FOR CARMICHAEL NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 13 February 2020, pp. 379-388
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
APPLICATIONS OF SYSTEMS OF QUADRATIC FORMS TO GENERALISED QUADRATIC FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 13 February 2020, pp. 374-386
- Print publication:
- December 2020
-
- Article
- Export citation
ON THE LONGEST BLOCK FUNCTION IN CONTINUED FRACTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 13 February 2020, pp. 196-206
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
PROOF OF TWO CONJECTURES ON SUPERCONGRUENCES INVOLVING CENTRAL BINOMIAL COEFFICIENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 13 February 2020, pp. 360-364
- Print publication:
- December 2020
-
- Article
- Export citation
On intrinsic and extrinsic rational approximation to Cantor sets
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 10 February 2020, pp. 1560-1589
- Print publication:
- May 2021
-
- Article
- Export citation
Generalized Beilinson Elements and Generalized Soulé Characters
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 06 February 2020, pp. 542-571
- Print publication:
- April 2021
-
- Article
- Export citation
PRIMES REPRESENTED BY INCOMPLETE NORM FORMS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 06 February 2020, e3
-
- Article
-
- You have access
- Open access
- Export citation
Ordinary primes in Hilbert modular varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 4 / April 2020
- Published online by Cambridge University Press:
- 06 February 2020, pp. 647-678
- Print publication:
- April 2020
-
- Article
- Export citation
UNIFORM ASYMPTOTIC FORMULAS FOR RESTRICTED BIPARTITE PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 05 February 2020, pp. 217-225
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
DEGREE-ONE MAHLER FUNCTIONS: ASYMPTOTICS, APPLICATIONS AND SPECULATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 05 February 2020, pp. 399-409
- Print publication:
- December 2020
-
- Article
- Export citation
Hypergeometric rational approximations to ζ(4)
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 03 February 2020, pp. 374-397
-
- Article
-
- You have access
- Open access
- Export citation
Limiting Properties of the Distribution of Primes in an Arbitrarily Large Number of Residue Classes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 30 January 2020, pp. 837-849
- Print publication:
- December 2020
-
- Article
- Export citation
Primitive Points in Rational Polygons
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 30 January 2020, pp. 850-870
- Print publication:
- December 2020
-
- Article
- Export citation
Ideal Uniform Polyhedra in
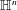 $\mathbb{H}^{n}$ and Covolumes of Higher Dimensional Modular Groups
$\mathbb{H}^{n}$ and Covolumes of Higher Dimensional Modular Groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 27 January 2020, pp. 465-492
- Print publication:
- April 2021
-
- Article
- Export citation
COMPARISON OF LOCAL RELATIVE CHARACTERS AND THE ICHINO–IKEDA CONJECTURE FOR UNITARY GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 22 January 2020, pp. 1803-1854
- Print publication:
- November 2021
-
- Article
- Export citation
MOMENTS OF RANDOM MULTIPLICATIVE FUNCTIONS, I: LOW MOMENTS, BETTER THAN SQUAREROOT CANCELLATION, AND CRITICAL MULTIPLICATIVE CHAOS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 20 January 2020, e1
-
- Article
-
- You have access
- Open access
- Export citation
OVERPARTITIONS RELATED TO THE MOCK THETA FUNCTION
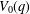 $V_{0}(q)$
$V_{0}(q)$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 16 January 2020, pp. 410-417
- Print publication:
- December 2020
-
- Article
- Export citation
ON LINEAR RELATIONS FOR DIRICHLET SERIES FORMED BY RECURSIVE SEQUENCES OF SECOND ORDER
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 110 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 16 January 2020, pp. 406-430
- Print publication:
- June 2021
-
- Article
- Export citation
Lower bound for the Perron–Frobenius degrees of Perron numbers
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 14 January 2020, pp. 1264-1280
- Print publication:
- April 2021
-
- Article
- Export citation
Bernoulli decomposition and arithmetical independence between sequences
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 14 January 2020, pp. 1590-1600
- Print publication:
- May 2021
-
- Article
-
- You have access
- Open access
- Export citation