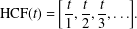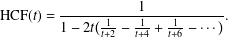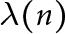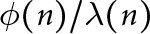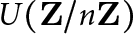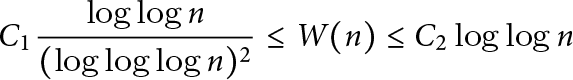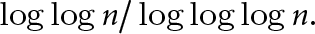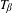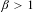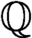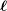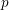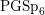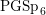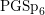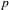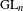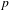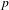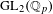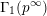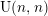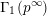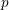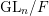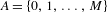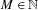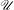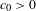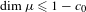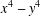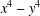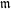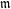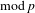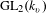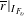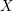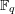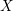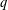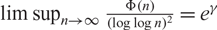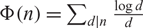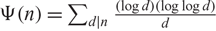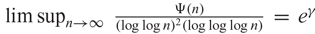Refine listing
Actions for selected content:
2812 results in 11xxx
AN EXACT FORMULA FOR THE HARMONIC CONTINUED FRACTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 10 June 2020, pp. 11-21
- Print publication:
- February 2021
-
- Article
- Export citation
The Number of Non-cyclic Sylow Subgroups of the Multiplicative Group Modulo n
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 08 June 2020, pp. 204-215
- Print publication:
- March 2021
-
- Article
- Export citation
Smale endomorphisms over graph-directed Markov systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 08 June 2020, pp. 2508-2541
- Print publication:
- August 2021
-
- Article
- Export citation
Primitive rational points on expanding horocycles in products of the modular surface with the torus
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 04 June 2020, pp. 1706-1750
- Print publication:
- June 2021
-
- Article
- Export citation
THE EXPONENTIAL DIOPHANTINE PROBLEM FOR
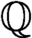 ${\mathbb {Q}}$
${\mathbb {Q}}$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 21 July 2020, pp. 671-672
- Print publication:
- June 2020
-
- Article
- Export citation
Corrigendum: Around
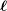 $\boldsymbol{\ell }$-independence
$\boldsymbol{\ell }$-independence
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 29 May 2020, pp. 1262-1274
- Print publication:
- June 2020
-
- Article
-
- You have access
- HTML
- Export citation
An exceptional Siegel–Weil formula and poles of the Spin L-function of
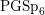 $\text{PGSp}_{6}$
$\text{PGSp}_{6}$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 29 May 2020, pp. 1231-1261
- Print publication:
- June 2020
-
- Article
- Export citation
A CLASS OF NONHOLOMORPHIC MODULAR FORMS II: EQUIVARIANT ITERATED EISENSTEIN INTEGRALS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 28 May 2020, e31
-
- Article
-
- You have access
- Open access
- Export citation
PATCHING AND THE COMPLETED HOMOLOGY OF LOCALLY SYMMETRIC SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 27 May 2020, pp. 395-458
- Print publication:
- March 2022
-
- Article
- Export citation
Shimura varieties at level
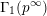 $\unicode[STIX]{x1D6E4}_{1}(p^{\infty })$ and Galois representations
$\unicode[STIX]{x1D6E4}_{1}(p^{\infty })$ and Galois representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 26 May 2020, pp. 1152-1230
- Print publication:
- June 2020
-
- Article
- Export citation
Relative bifurcation sets and the local dimension of univoque bases
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 26 May 2020, pp. 2241-2273
- Print publication:
- August 2021
-
- Article
- Export citation
Maximizing Bernoulli measures and dimension gaps for countable branched systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 26 May 2020, pp. 1921-1939
- Print publication:
- July 2021
-
- Article
- Export citation
PERIOD IDENTITIES OF CM FORMS ON QUATERNION ALGEBRAS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 20 May 2020, e25
-
- Article
-
- You have access
- Open access
- Export citation
INTEGERS REPRESENTED BY
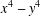 $x^{4}-y^{4}$ REVISITED
$x^{4}-y^{4}$ REVISITED
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 20 May 2020, pp. 38-49
- Print publication:
- February 2021
-
- Article
- Export citation
The size of the primes obstructing the existence of rational points
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 15 May 2020, pp. 652-704
- Print publication:
- April 2021
-
- Article
- Export citation
MULTIPLICITY ONE AT FULL CONGRUENCE LEVEL
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 15 May 2020, pp. 637-658
- Print publication:
- March 2022
-
- Article
- Export citation
Möbius Randomness Law for Frobenius Traces of Ordinary Curves
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 15 May 2020, pp. 192-203
- Print publication:
- March 2021
-
- Article
- Export citation
Cuspidal cohomology of stacks of shtukas
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 14 May 2020, pp. 1079-1151
- Print publication:
- June 2020
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SUMS OF PARTIAL THETA FUNCTIONS THROUGH AN EXTENDED BAILEY TRANSFORM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 13 May 2020, pp. 1-10
- Print publication:
- February 2021
-
- Article
- Export citation
AN EXTENSION OF A RESULT OF ERDŐS AND ZAREMBA
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 13 May 2020, pp. 193-222
- Print publication:
- January 2021
-
- Article
- Export citation