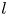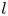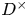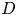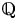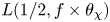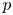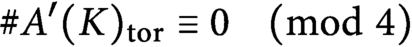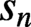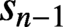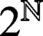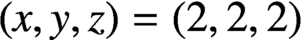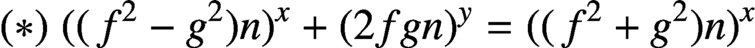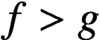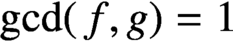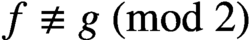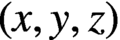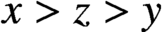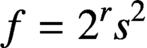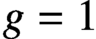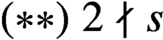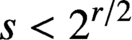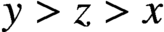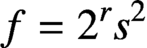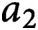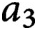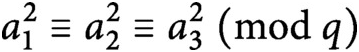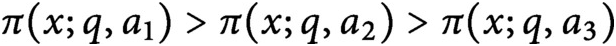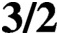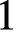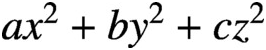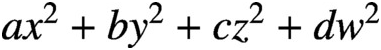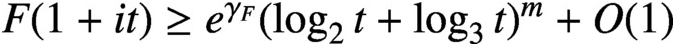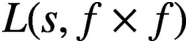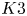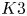Refine listing
Actions for selected content:
2812 results in 11xxx
Mixed Ax–Schanuel for the universal abelian varieties and some applications
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 11 December 2020, pp. 2263-2297
- Print publication:
- November 2020
-
- Article
- Export citation
Automorphy lifting for residually reducible
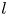 $l$-adic Galois representations, II
$l$-adic Galois representations, II
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 15 December 2020, pp. 2399-2422
- Print publication:
- November 2020
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sup-norms of eigenfunctions in the level aspect for compact arithmetic surfaces, II: newforms and subconvexity
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 15 December 2020, pp. 2368-2398
- Print publication:
- November 2020
-
- Article
- Export citation
Branching laws for classical groups: the non-tempered case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 17 December 2020, pp. 2298-2367
- Print publication:
- November 2020
-
- Article
- Export citation
ONE-LEVEL DENSITY OF LOW-LYING ZEROS OF QUADRATIC HECKE L-FUNCTIONS OF IMAGINARY QUADRATIC NUMBER FIELDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 29 October 2020, pp. 170-192
- Print publication:
- April 2022
-
- Article
- Export citation
Divisibility of torsion subgroups of abelian surfaces over number fields
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 28 October 2020, pp. 266-298
- Print publication:
- February 2022
-
- Article
- Export citation
CLASS NUMBERS OF CM ALGEBRAIC TORI, CM ABELIAN VARIETIES AND COMPONENTS OF UNITARY SHIMURA VARIETIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 245 / March 2022
- Published online by Cambridge University Press:
- 28 October 2020, pp. 74-99
- Print publication:
- March 2022
-
- Article
- Export citation
Autocorrelation functions for quantum particles in supersymmetric Pöschl-Teller potentials
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 28 October 2020, pp. 840-852
- Print publication:
- December 2021
-
- Article
- Export citation
LOOK, KNAVE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 21 October 2020, pp. 210-217
- Print publication:
- April 2021
-
- Article
- Export citation
A NOTE ON JEŚMANOWICZ’ CONJECTURE CONCERNING NONPRIMITIVE PYTHAGOREAN TRIPLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 21 October 2020, pp. 29-39
- Print publication:
- August 2021
-
- Article
- Export citation
DISTRIBUTION OF INTEGERS WITH PRESCRIBED STRUCTURE AND APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 19 October 2020, pp. 509-511
- Print publication:
- June 2021
-
- Article
-
- You have access
- Export citation
Densities in certain three-way prime number races
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 12 October 2020, pp. 232-265
- Print publication:
- February 2022
-
- Article
- Export citation
Newman's identities, lucas sequences and congruences for certain partition functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 3 / August 2020
- Published online by Cambridge University Press:
- 08 October 2020, pp. 709-736
-
- Article
- Export citation
Popular differences for corners in Abelian groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 1 / July 2021
- Published online by Cambridge University Press:
- 07 October 2020, pp. 207-225
- Print publication:
- July 2021
-
- Article
- Export citation
Uniform convergence rate for Birkhoff means of certain uniquely ergodic toral maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 06 October 2020, pp. 3363-3388
- Print publication:
- November 2021
-
- Article
- Export citation
CONGRUENCES MODULO 4 FOR WEIGHT
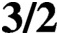 $\textbf{3/2}$ ETA-PRODUCTS
$\textbf{3/2}$ ETA-PRODUCTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 05 October 2020, pp. 405-417
- Print publication:
- June 2021
-
- Article
- Export citation
POINTS OF SMALL HEIGHT ON AFFINE VARIETIES DEFINED OVER FUNCTION FIELDS OF FINITE TRANSCENDENCE DEGREE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 05 October 2020, pp. 418-427
- Print publication:
- June 2021
-
- Article
- Export citation
PRIME-UNIVERSAL DIAGONAL QUADRATIC FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 05 October 2020, pp. 390-404
- Print publication:
- June 2021
-
- Article
- Export citation
LARGE VALUES OF L-FUNCTIONS ON THE 1-LINE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 02 October 2020, pp. 230-243
- Print publication:
- April 2021
-
- Article
- Export citation
K3 surfaces with involution, equivariant analytic torsion, and automorphic forms on the moduli space IV: The structure of the invariant
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 10 / October 2020
- Published online by Cambridge University Press:
- 19 November 2020, pp. 1965-2019
- Print publication:
- October 2020
-
- Article
- Export citation