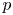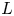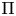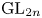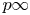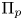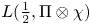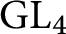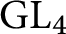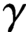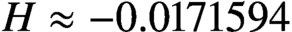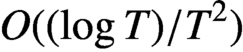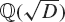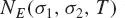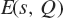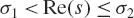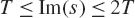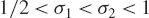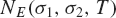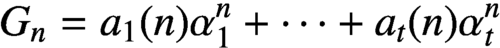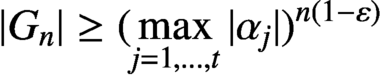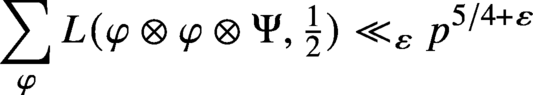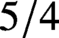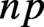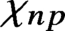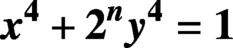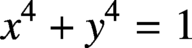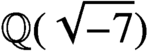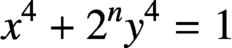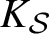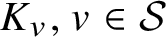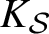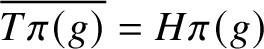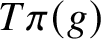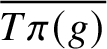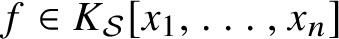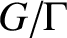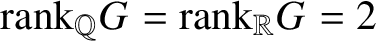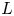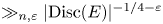Refine listing
Actions for selected content:
2812 results in 11xxx
L-functions of GL2n: p-adic properties and non-vanishing of twists
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 08 January 2021, pp. 2437-2468
- Print publication:
- December 2020
-
- Article
- Export citation
NOTES ON THE K-RATIONAL DISTANCE PROBLEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 01 December 2020, pp. 40-44
- Print publication:
- August 2021
-
- Article
- Export citation
A proof of the linear Arithmetic Fundamental Lemma for
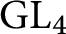 $ \operatorname {{\mathrm {GL}}}_4$
$ \operatorname {{\mathrm {GL}}}_4$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 23 November 2020, pp. 381-427
- Print publication:
- April 2022
-
- Article
- Export citation
Directions in orbits of geometrically finite hyperbolic subgroups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 2 / September 2021
- Published online by Cambridge University Press:
- 23 November 2020, pp. 277-316
- Print publication:
- September 2021
-
- Article
- Export citation
A HARMONIC SUM OVER NONTRIVIAL ZEROS OF THE RIEMANN ZETA-FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 20 November 2020, pp. 59-65
- Print publication:
- August 2021
-
- Article
- Export citation
Zeros of the Epstein zeta function to the right of the critical line
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 2 / September 2021
- Published online by Cambridge University Press:
- 17 November 2020, pp. 265-276
- Print publication:
- September 2021
-
- Article
- Export citation
Generic Newton points and the Newton poset in Iwahori-double cosets
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 13 November 2020, e50
-
- Article
-
- You have access
- Open access
- Export citation
Profinite invariants of arithmetic groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 13 November 2020, e54
-
- Article
-
- You have access
- Open access
- Export citation
On the prime factors of the iterates of the Ramanujan τ–function
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 4 / November 2020
- Published online by Cambridge University Press:
- 11 November 2020, pp. 1031-1047
-
- Article
- Export citation
ON UNRAMIFIED SOLVABLE EXTENSIONS OF SMALL NUMBER FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 09 November 2020, pp. 428-437
- Print publication:
- June 2021
-
- Article
- Export citation
ON THE GROWTH OF LINEAR RECURRENCES IN FUNCTION FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 09 November 2020, pp. 11-20
- Print publication:
- August 2021
-
- Article
-
- You have access
- Open access
- Export citation
EXPONENTIAL SUMS AND ADDITIVE COMBINATORICS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 09 November 2020, pp. 506-508
- Print publication:
- June 2021
-
- Article
-
- You have access
- Export citation
Bounds for twisted symmetric square L-functions via half-integral weight periods
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 09 November 2020, e44
-
- Article
-
- You have access
- Open access
- Export citation
THE DIOPHANTINE EQUATION
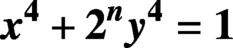 $\boldsymbol{x}^{\boldsymbol{4}} \boldsymbol{+} \boldsymbol{2}^{\boldsymbol{n}}\boldsymbol{y}^{\boldsymbol{4}} \boldsymbol{=} \boldsymbol{1}$ IN QUADRATIC NUMBER FIELDS
$\boldsymbol{x}^{\boldsymbol{4}} \boldsymbol{+} \boldsymbol{2}^{\boldsymbol{n}}\boldsymbol{y}^{\boldsymbol{4}} \boldsymbol{=} \boldsymbol{1}$ IN QUADRATIC NUMBER FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 06 November 2020, pp. 21-28
- Print publication:
- August 2021
-
- Article
- Export citation
Erratum: Limiting properties of the distribution of primes in an arbitrarily large number of residue classes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 05 November 2020, pp. 1041-1044
- Print publication:
- December 2021
-
- Article
-
- You have access
- Export citation
Closures of locally divergent orbits of maximal tori and values of homogeneous forms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 05 November 2020, pp. 3142-3177
- Print publication:
- October 2021
-
- Article
- Export citation
Divergent trajectories in arithmetic homogeneous spaces of rational rank two
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 05 November 2020, pp. 3116-3141
- Print publication:
- October 2021
-
- Article
-
- You have access
- Open access
- Export citation
Number-theoretic positive entropy shifts with small centralizer and large normalizer
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 04 November 2020, pp. 3201-3226
- Print publication:
- November 2021
-
- Article
-
- You have access
- Open access
- Export citation
Vanishing theorems for the mod p cohomology of some simple Shimura varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 03 November 2020, e38
-
- Article
-
- You have access
- Open access
- Export citation
Non-vanishing of class group L-functions for number fields with a small regulator
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 17 December 2020, pp. 2423-2436
- Print publication:
- November 2020
-
- Article
- Export citation