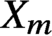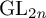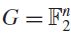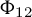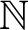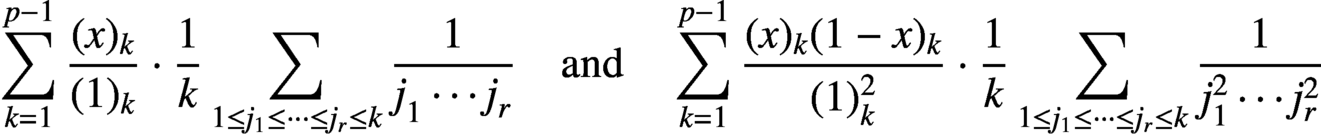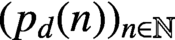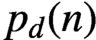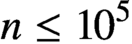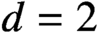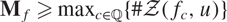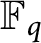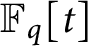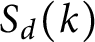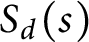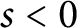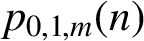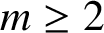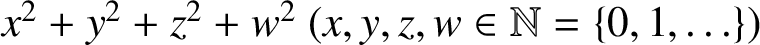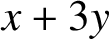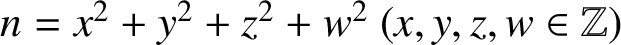Refine listing
Actions for selected content:
2812 results in 11xxx
Prime number theorem for regular Toeplitz subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 4 / April 2022
- Published online by Cambridge University Press:
- 15 February 2021, pp. 1446-1473
- Print publication:
- April 2022
-
- Article
- Export citation
Nonspecial varieties and generalised Lang–Vojta conjectures
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 10 February 2021, e11
-
- Article
-
- You have access
- Open access
- Export citation
RAISING THE LEVEL OF AUTOMORPHIC REPRESENTATIONS OF
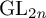 $\mathrm {GL}_{2n}$ OF UNITARY TYPE
$\mathrm {GL}_{2n}$ OF UNITARY TYPE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 09 February 2021, pp. 1421-1444
- Print publication:
- July 2022
-
- Article
-
- You have access
- Open access
- Export citation
On the Skolem problem and some related questions for parametric families of linear recurrence sequences
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 08 February 2021, pp. 773-792
- Print publication:
- June 2022
-
- Article
- Export citation
A variant of the Corners theorem
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 3 / November 2021
- Published online by Cambridge University Press:
- 02 February 2021, pp. 607-621
- Print publication:
- November 2021
-
- Article
- Export citation
KODAIRA DIMENSION OF UNIVERSAL HOLOMORPHIC SYMPLECTIC VARIETIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 02 February 2021, pp. 1849-1866
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- Export citation
Le transfert singulier pour la formule des traces de Jacquet–Rallis
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 16 March 2021, pp. 303-434
- Print publication:
- February 2021
-
- Article
- Export citation
CONGRUENCE OF ULTRAFILTERS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 746-761
- Print publication:
- June 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Curves on K3 surfaces in divisibility 2
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 01 February 2021, e9
-
- Article
-
- You have access
- Open access
- Export citation
The number of maximum primitive sets of integers
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 28 January 2021, pp. 781-795
-
- Article
- Export citation
TWO SUPERCONGRUENCES RELATED TO MULTIPLE HARMONIC SUMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 28 January 2021, pp. 379-389
- Print publication:
- June 2021
-
- Article
- Export citation
SOME OBSERVATIONS AND SPECULATIONS ON PARTITIONS INTO d-TH POWERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 28 January 2021, pp. 406-414
- Print publication:
- December 2021
-
- Article
-
- You have access
- Open access
- Export citation
IHARA LEMMA AND LEVEL RAISING IN HIGHER DIMENSION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 25 January 2021, pp. 1701-1726
- Print publication:
- September 2022
-
- Article
- Export citation
ON GOOD APPROXIMATIONS AND THE BOWEN–SERIES EXPANSION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 25 January 2021, pp. 45-58
- Print publication:
- August 2021
-
- Article
- Export citation
Primitive prime divisors in the critical orbits of one-parameter families of rational polynomials
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 3 / November 2021
- Published online by Cambridge University Press:
- 25 January 2021, pp. 569-584
- Print publication:
- November 2021
-
- Article
- Export citation
EXTREMAL CASES OF RAPOPORT–ZINK SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 20 January 2021, pp. 1727-1782
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- Export citation
Vanishing of multizeta values over
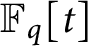 $\mathbb {F}_q[t]$ at negative integers
$\mathbb {F}_q[t]$ at negative integers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 18 January 2021, pp. 9-29
- Print publication:
- March 2022
-
- Article
-
- You have access
- Open access
- Export citation
BIASES IN INTEGER PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 14 January 2021, pp. 177-186
- Print publication:
- October 2021
-
- Article
- Export citation
SUMS OF FOUR SQUARES WITH A CERTAIN RESTRICTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 14 January 2021, pp. 218-227
- Print publication:
- October 2021
-
- Article
- Export citation
Boxes, extended boxes and sets of positive upper density in the Euclidean space
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 3 / November 2021
- Published online by Cambridge University Press:
- 14 January 2021, pp. 481-501
- Print publication:
- November 2021
-
- Article
-
- You have access
- Open access
- Export citation