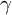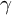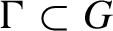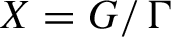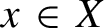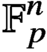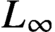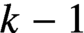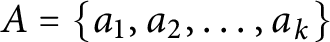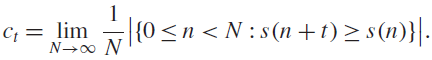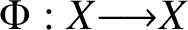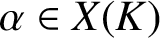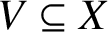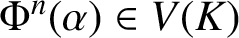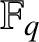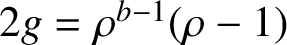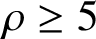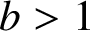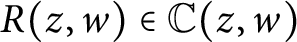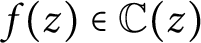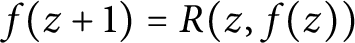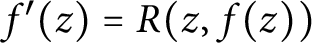Refine listing
Actions for selected content:
2812 results in 11xxx
A NEW REFINEMENT OF FINE’S PARTITION THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 29 March 2021, pp. 353-361
- Print publication:
- December 2021
-
- Article
- Export citation
ADDITIVE BASES AND NIVEN NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 25 March 2021, pp. 373-380
- Print publication:
- December 2021
-
- Article
- Export citation
ON A WEIGHTED SUM OF MULTIPLE $\mathbf{{T}}$
 -VALUES OF FIXED WEIGHT AND DEPTH
-VALUES OF FIXED WEIGHT AND DEPTH
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 19 March 2021, pp. 398-405
- Print publication:
- December 2021
-
- Article
- Export citation
ON FORMAL DEGREES OF UNIPOTENT REPRESENTATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 19 March 2021, pp. 1947-1999
- Print publication:
- November 2022
-
- Article
- Export citation
Non-dense orbits on homogeneous spaces and applications to geometry and number theory
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 4 / April 2022
- Published online by Cambridge University Press:
- 18 March 2021, pp. 1327-1372
- Print publication:
- April 2022
-
- Article
- Export citation
SPECIAL VALUES OF THE ZETA FUNCTION OF AN ARITHMETIC SURFACE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 15 March 2021, pp. 2043-2091
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- Export citation
Extending tamely ramified strict 1-motives into két log 1-motives
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 09 March 2021, e20
-
- Article
-
- You have access
- Open access
- Export citation
High-entropy dual functions over finite fields and locally decodable codes
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 08 March 2021, e19
-
- Article
-
- You have access
- Open access
- Export citation
R-GROUP AND WHITTAKER SPACE OF SOME GENUINE REPRESENTATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 08 March 2021, pp. 213-273
- Print publication:
- January 2023
-
- Article
- Export citation
ON FUNDAMENTAL FOURIER COEFFICIENTS OF SIEGEL MODULAR FORMS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 03 March 2021, pp. 2001-2041
- Print publication:
- November 2022
-
- Article
- Export citation
Overconvergent modular forms are highest-weight vectors in the Hodge-Tate weight zero part of completed cohomology
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 02 March 2021, e17
-
- Article
-
- You have access
- Open access
- Export citation
Depth-graded motivic multiple zeta values
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 22 March 2021, pp. 529-572
- Print publication:
- March 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamical and arithmetic degrees for random iterations of maps on projective space
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 2 / September 2021
- Published online by Cambridge University Press:
- 26 February 2021, pp. 369-385
- Print publication:
- September 2021
-
- Article
- Export citation
Sumsets of semiconvex sets
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 26 February 2021, pp. 84-94
- Print publication:
- March 2022
-
- Article
- Export citation
A lower bound for Cusick’s conjecture on the digits of n + t
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 24 February 2021, pp. 139-161
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- Export citation
A SPARSITY RESULT FOR THE DYNAMICAL MORDELL–LANG CONJECTURE IN POSITIVE CHARACTERISTIC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 23 February 2021, pp. 381-390
- Print publication:
- December 2021
-
- Article
- Export citation
NONNEGATIVE POLYNOMIALS, SUMS OF SQUARES AND THE MOMENT PROBLEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 19 February 2021, pp. 337-341
- Print publication:
- October 2021
-
- Article
-
- You have access
- Export citation
CHARACTERISTIC POLYNOMIALS OF SIMPLE ORDINARY ABELIAN VARIETIES OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 19 February 2021, pp. 391-397
- Print publication:
- December 2021
-
- Article
- Export citation
Effective finiteness of solutions to certain differential and difference equations
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 16 February 2021, pp. 52-67
- Print publication:
- March 2022
-
- Article
- Export citation
Eigenfunctions of the Fourier transform with specified zeros
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 2 / September 2021
- Published online by Cambridge University Press:
- 15 February 2021, pp. 329-367
- Print publication:
- September 2021
-
- Article
- Export citation