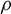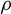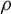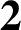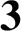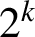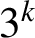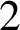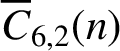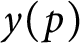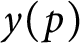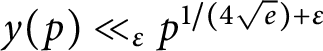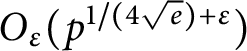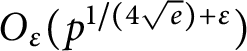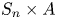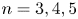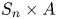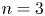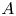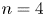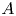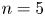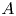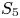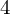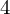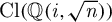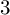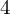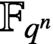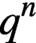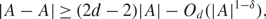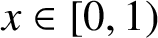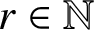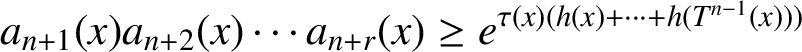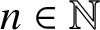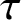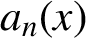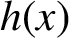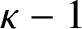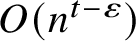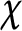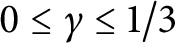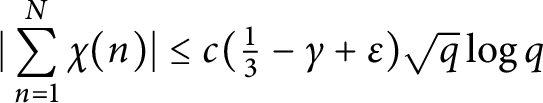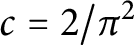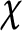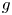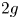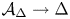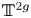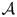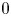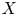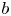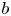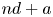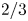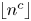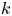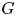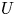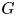Refine listing
Actions for selected content:
2812 results in 11xxx
THE COHOMOLOGY OF UNRAMIFIED RAPOPORT–ZINK SPACES OF EL-TYPE AND HARRIS’S CONJECTURE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 14 January 2021, pp. 1163-1218
- Print publication:
- July 2022
-
- Article
-
- You have access
- Open access
- Export citation
DIVISIBILITY OF CERTAIN SINGULAR OVERPARTITIONS BY POWERS OF
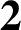 $\textbf{2}$ AND
$\textbf{2}$ AND 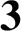 $\textbf{3}$
$\textbf{3}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 14 January 2021, pp. 238-248
- Print publication:
- October 2021
-
- Article
- Export citation
Subproducts of small residue classes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 13 January 2021, pp. 1-8
- Print publication:
- March 2022
-
- Article
- Export citation
The second moment of symmetric square L-functions over Gaussian integers
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 11 January 2021, pp. 54-80
- Print publication:
- February 2022
-
- Article
- Export citation
ON A FABRIC OF KISSING CIRCLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 08 January 2021, pp. 320-329
- Print publication:
- October 2021
-
- Article
- Export citation
ON A CERTAIN LOCAL IDENTITY FOR LAPID–MAO’S CONJECTURE AND FORMAL DEGREE CONJECTURE : EVEN UNITARY GROUP CASE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 08 January 2021, pp. 1107-1161
- Print publication:
- July 2022
-
- Article
- Export citation
Bounds for sets with no polynomial progressions
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 05 January 2021, e16
-
- Article
-
- You have access
- Open access
- Export citation
Malle's conjecture for
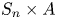 $S_n\times A$ for
$S_n\times A$ for 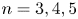 $n = 3,4,5$
$n = 3,4,5$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 15 February 2021, pp. 83-121
- Print publication:
- January 2021
-
- Article
- Export citation
EXTREME VALUES OF GEODESIC PERIODS ON ARITHMETIC HYPERBOLIC SURFACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 22 December 2020, pp. 1507-1542
- Print publication:
- September 2022
-
- Article
- Export citation
ON THE
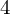 $4$-RANK OF CLASS GROUPS OF DIRICHLET BIQUADRATIC FIELDS
$4$-RANK OF CLASS GROUPS OF DIRICHLET BIQUADRATIC FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 22 December 2020, pp. 1543-1570
- Print publication:
- September 2022
-
- Article
- Export citation
MÖBIUS–FROBENIUS MAPS ON IRREDUCIBLE POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 14 December 2020, pp. 66-77
- Print publication:
- August 2021
-
- Article
- Export citation
On a conjecture of Chen and Yui: Resultants and discriminants
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 14 December 2020, pp. 486-526
- Print publication:
- April 2022
-
- Article
- Export citation
Difference sets in higher dimensions
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 3 / November 2021
- Published online by Cambridge University Press:
- 14 December 2020, pp. 467-480
- Print publication:
- November 2021
-
- Article
- Export citation
ON THE SUM OF PARTS IN THE PARTITIONS OF n INTO DISTINCT PARTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 11 December 2020, pp. 228-237
- Print publication:
- October 2021
-
- Article
- Export citation
HAUSDORFF DIMENSION FOR THE SET OF POINTS CONNECTED WITH THE GENERALIZED JARNÍK–BESICOVITCH SET
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 07 December 2020, pp. 1-29
- Print publication:
- February 2022
-
- Article
- Export citation
Sarnak’s conjecture for sequences of almost quadratic word growth
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 04 December 2020, pp. 3060-3115
- Print publication:
- October 2021
-
- Article
-
- You have access
- Open access
- Export citation
A Pólya–Vinogradov inequality for short character sums
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 02 December 2020, pp. 906-910
- Print publication:
- December 2021
-
- Article
- Export citation
Generic rank of Betti map and unlikely intersections
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 12 January 2021, pp. 2469-2509
- Print publication:
- December 2020
-
- Article
-
- You have access
- HTML
- Export citation
The level of distribution of the Thue–Morse sequence
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 25 January 2021, pp. 2560-2587
- Print publication:
- December 2020
-
- Article
- Export citation
Arithmetic purity of strong approximation for semi-simple simply connected groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 01 February 2021, pp. 2628-2649
- Print publication:
- December 2020
-
- Article
- Export citation